Einleitung bovi2000,495

1

auto

• FBI -verwendet bereits Wavelets zur Fingerprintarchivierung
• JPEG2000 - der Nachfolger von JPEG verwendet Wavelets
• MPEG-4

2

auto

In den letzten Jahren war bezüglich Bildkompression immer mehr und mehr von Wavelets und Wavelettransformation die Rede. Die erste Institution, die Wavelets schließlich in die Praxis eingeführt hat, ist das FBI. Fingerabdrücke werden dort bereits mittels einer waveletbasierten Kompressionstechnik kodiert und archiviert. Auch der neue Bildkodierungsstandard JPEG2000, der mittelfristig den zurzeit allgegenwärtigen JPEG Standard ablösen soll, basiert auf der Wavelettransformation. Auch im MPEG-4 Standard kommt die waveletbasierte Bildkodierung zum Einsatz.

Was macht Wavelets für die Bildkodierung interessant?

1

Mehrfachauflösung der Wavelettransformation

• Wavelettransformation erzeugt Mehrfachauflösung des Bildes
  • Trotz Mehrauflösung keine zusätzlichen Datenmengen!
• Bilder geringerer Auflösung
  • Bildpunkte entstehen nicht durch Unterabtastung!
  • Bildpunkte sind Waveletkoffizienten
• Approximation der Originalauflösung
  • von jeder Auflösungstufe kann mit Wavelets volle Auflösung approximiert werden
  • Qualität Approximation hängt stark von verwendeter Mutterwavelet

Lena in Mehrfachauflösungen PC bovi2000

Lena in Mehrfachauflösungen PDA_Phonebovi2000

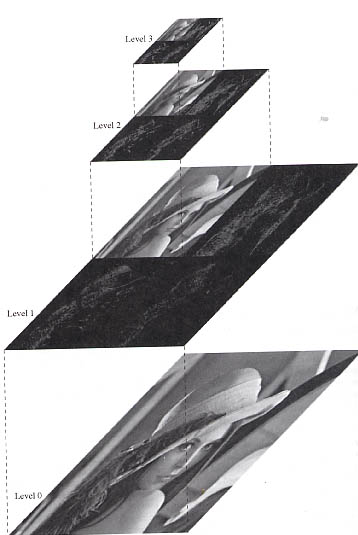
2

auto

Mit Hilfe der Wavelettransformation wird ein Bild in unterschiedlichen Auflösungsstufen dargestellt (siehe Lerneinheit Wavelets). An und für sich ist an dieser Eigenschaft nichts besonderes, denn es gibt viele und auch sehr triviale Verfahren, ein Bild in mehreren Auflösungsstufen darzustellen. Diesen Techniken ist aber allen gemeinsam, dass sie durch das Konzept der Mehrfachauflösung (englisch: muliresolution) zusätzliche Datenmengen erzeugen.

Mehrfachauflösung der Wavelettransformation

Das Außergewöhnliche an der Mehrfachauflösungstechnik der Wavelettransformation gegenüber anderen Techniken ist unter anderem, dass trotz der zusätzlichen Informationen die Datengröße unverändert bleibt. Weiters handelt es sich bei den Bildern mit geringerer Auflösung nicht einfach um Bilder, die durch Unterabtastung der Bildpunkte des Originalbildes entstanden sind. Vielmehr stellen ihre Bildpunkte Waveletkoeffizienten (siehe Lerneinheit Wavelets) dar, mit deren Hilfe man eine Approximation des Originalbildes in Originalauflösung erzeugen kann. Die Qualität dieser Approximation hängt entscheidend davon ab, welche Mutterwavelet bei der Transformation verwendet worden ist. Im Folgenden soll die Mehrfachauflösung und dessen Funktion zur Bilddatenkompression an hand eines Beispieles (Bild wird in 3 Auflösungsstufen repräsentiert) erläutert werden.

Lena in Mehrfachauflösungen PCbovi2000

• Level 0 - ist das unkomprimierte Originalbild in voller Auflösung.
• Level 1- Layer 1 erhält man durch die Wavelettransformation, angewandt auf das Originalbild. Die Gesamtpixelanzahl bleibt durch die Transformation unverändert. Das Bild selber (linkes oberes Viertel) beansprucht nur mehr ein Viertel der Gesamtpixelanzahl. Dieses Bild ist eine „gesoftete“ Version des Originalbildes, die Bildpunkte stellen die Waveletkoeffizienten dar. Die übrigen Bildteile von Layer 1 beinhalten Detailinformationen, mit deren Hilfe man aus dem gesofteten Bild das Originalbild verlustfrei rekonstruieren kann.
• Level 2 und 3 - Zur Erzeugung weiterer Auflösungsstufen wird die gleiche Prozedur auf das Bild des vorhergehenden Layers angewandt.

Lena in Mehrfachauflösungen PDA_Phonebovi2000

• Level 0 - ist das unkomprimierte Originalbild in voller Auflösung.
• Level 1- Layer 1 erhält man durch die Wavelettransformation, angewandt auf das Originalbild. Die Gesamtpixelanzahl bleibt durch die Transformation unverändert. Das Bild selber (linkes oberes Viertel) beansprucht nur mehr ein Viertel der Gesamtpixelanzahl. Dieses Bild ist eine „gesoftete“ Version des Originalbildes, die Bildpunkte stellen die Waveletkoeffizienten dar. Die übrigen Bildteile von Layer 1 beinhalten Detailinformationen, mit deren Hilfe man aus dem gesofteten Bild das Originalbild verlustfrei rekonstruieren kann.
• Level 2 und 3 - Zur Erzeugung weiterer Auflösungsstufen wird die gleiche Prozedur auf das Bild des vorhergehenden Layers angewandt.

Filterbänke bovi2000

1

Grundfilter

• Drei Gundfilter
  • Hochpass
  • Tiefpass
  • Bandpass

Pulsantwort

• Filtereingang Impulssignal
• Filterausgang Pulsantwort
• Waveletfilter
  • Wavelet ist Pulsantwort

Filterbank

• Filterbank
  • besteht aus mehreen Grundfiltern
  • Es gehen keine Frquenzkomponenten verloren
• Analytische Filterbank
  • Teilt ein Signal in mehrere Frequenzbänder
• Synthetische Filterbank
  • generiert aus Frequnenzbändern ein Signal

Analytische Filterbank PC

Analytische Filterbank PDA_Phone

Synthetische Filterbank PC

Synthetische Filterbank PDA_Phone

Unterabtasten bei digitalen Filterbänken

• Unterabtasten Allgemein
  • Summe der Abtastraten der Frequenzbänder = Abtastrate des Eingangsignals
  • Ergo -Filterbank erzeugt keine zusätzlichen Daten
• Zweistufige Filterbank
  • Abtastrate am Eingang durch Eingangssignal festgelegt
  • Abtastrate am Ausgang jeweils halbiert
• Zusammenhang mit Nyquest- Shannon Theorem ableitbar

Unterabtastung bei zwei Frequenzbänder PC

Unterabtastung bei zwei Frequenzbänder PC

2

Bei eingehender Betrachtung stellt man fest, dass die Wavelettransformation eine spezielle Art von Filterbank ist. Um die waveletbasierte Bildkodierung genauer verstehen zu können, muss man sich daher zuerst mit den Prinzipien von Filterbanken vertraut machen.

Grundfilter

Es gibt prinzipielle drei Grundfilter: Hochpass-, Tiefpass- und Bandpass. Alle drei werden durch den Parameter Grenzfrequenz spezifiziert.

• Hochpass (HP)– Alle Frequenzen, die oberhalb der Grenzfrequenz liegen, passieren das Filter, die tiefen Frequenzen werden gesperrt.
• Tiefpass (TP)– Alle Frequenzen, die unterhalb der Grenzfrequenz liegen, passieren ungehindert das Filter, alle darüber liegenden Frequenzen werden gesperrt.
• Bandpass (BP)– Das Bandpass Filter hat zwei Grenzfrequenzen. Frequenzen, die innerhalb der Grenzewerte liegen, können passieren, alle anderen werden gesperrt.

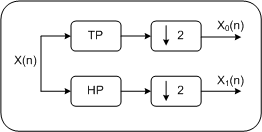
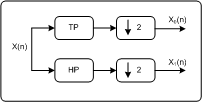
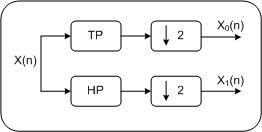
All den Filtern ist gemeinsam, dass sie Signale erzeugen, die sich nur aus einem speziellen Teil des Frequenzspektrums des Originalsignals aufbauen. Diese Teilsignale bezeichnet man als Frequenzbänder des Originalsignals. Neben der Grenzfrequenz haben Filter noch weitere Spezifikationen. Im Zusammenhang der Wavelettransformation ist die Pulsantwort eines Filters von elementarer Bedeutung.

Pulsantwort

Legt man an den Eingang eines Filters einen kurzen Impuls (theoretisch von unendlich kurzer Dauer und unendlich hoher Amplitude), so erhält man am Ausgang ein für den Filter charakteristisches Zeitsignal, die Impulsantwort. Bei der Wavelettransformation entsprechen die Pulsantworten den Wavelets.

Filterbank

Hier unterscheidet man zwischen analytischer und synthetischer Filterbank. Eine analytische Filterbank teilt mit Hilfe einer Gruppe von Grundfiltern ein Signal in mehrere Frequenzbänder. In Summe gehen aber dabei im Gegensatz zu einzelnen Grundfiltern keine Frequenzanteile verloren, sondern es ist die gesamte Information jeglich auf mehrere Frequenzbänder aufgeteilt. Die synthetische Filterbank macht das umgekehrte: Aus den Frequenzbändern wird ein Signal generiert. Bei verlustfrei arbeitenden Filterbanken entspricht das Signal am Ausgang der synthetischen Filterbank dem Originalsignal. Je nach Anwendung kann eine Filterbank ein Signal in beliebig viele Frequenzbänder teilen. Im Folgenden werden nur Filterbänke, die das Signal in zwei Frequenzbänder teilen, betrachtet, da die Wavelettransformation als eine Kaskade solcher Filterbänke verstanden werden kann. Für die Wavelettransformation entspricht die Transformation des Originalssignals einer analytischen Filterbank, die inverse bzw Rücktransformation einer synthetischen Filterbank.

Analytische, zweistufige Filterbank PC

Eine Filterbank teilt das Originalsignal in zwei Frequenzbänder. Bei der Wavelettransformation umfasst ein Frequenzband jeweils die Hälfte des gesamten Frequenzbereiches.

Analytische, zweistufige Filterbank PDA_Phone

Eine Filterbank teilt das Originalsignal in zwei Frequenzbänder. Bei der Wavelettransformation umfasst ein Frequenzband jeweils die Hälfte des gesamten Frequenzbereiches.

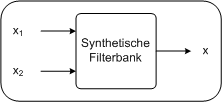
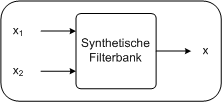
Das durch das Tiefpass erzeugte Signal enthält die tiefen Frequenzen des Signals. Das durch das Hochpass erzeugte Signal enthält die hohen Frequenzen des Signals. Die Grenzfrequenz ist für beide Filter gleich. Sie liegt genau in der Mitte des Frequenzspektrums des Originalsignals.

Synthetische, zweistufige Filterbank PC

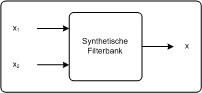
Synthetische, zweistufige Filterbank PDA_Phone

In der synthetischen Filterbank werden die Frequenzbänder zusammengefügt. Arbeiten die Algorithmen der Filterbank verlustfrei, ist das Ausgangssignal der synthetischen Filterbank ident mit dem Signal am Eingang der analytischen Filterbank.

Unterabtasten bei digitalen Filterbänken

Für die Bildkodierung betrachten wir hier ausschließlich digitale Bilder, also sind auch unsere Signale rein digital. Das Eingangsignal an der analytischen Filterbank ist nun mit einer bestimmten Abtastfrequenz festgelegt. Die zweistufige Filterbank erzeugt daraus zwei digitale Signale. Die beiden Ausgangssignale haben dabei jeweils nur eine halb so große Abtastfrequenz wie das Eingangssignal. Das heißt zum Beispiel, für 4 Abtastwerte am Eingang werden 2 Abtastwerte für das tieffrequente Band und zwei für das hochfrequente Band generiert. In Summe sind es wieder 4 Abtastwerte. Die Filterbank verursacht also keine Änderung der Datenmenge. Diese Eigenschaft lässt sich leicht aus dem Nyquest- Shannon Theorem ableiten. Durch den Filtervorgang hat jedes Frequenzband nur mehr die Hälfte der Bandbreite des Eingangsignals. Wird die Bandbreite halbiert, so wird nach Shannon auch die erforderliche Abtastrate halbiert.

Unterabtastung bei zwei Frequenzbänder PC

Unterabtastung bei zwei Frequenzbänder PDA_Phone

Unterabtastung bei Filterbank mit zwei Frequenzbändern. die beiden Signale am Ausgang haben jeweils die Halbe abtastfrequenz des Einganassignals.

Filterbank für 2 dimensionale Bildsignale kana2004

1

Filterung der Spalten (vertikale Filterung) PC

Filterung der Zeilen (horizontale Filterung) PC

Filterung der Spalten (vertikale Filterung) PDA_Phone

Filterung der Zeilen (horizontale Filterung) PDA_Phone

2

Filterung zweidimensionaler Signale

Bisher wurden nur Filterbanken für eindimensionale Signale betrachtet. Bei Bildern handelt es sich aber um zweidimensionale Signale. Für die Wavelettransformation solcher Signale werden Zeilen und Spalten separat als eigenes Signal betrachtet.

Filterung der Spalten (vertikale Filterung) PC

Es werden die Spalten zu einem eindimensionalen Signal zusammengefasst, und in zwei Frequenzbänder geteilt. Das untere Frequenzband (TP 509) zeigt ein Bild, dessen horizontale Kanten gegenüber dem Originalbild unschärfer dargestellt sind, das obere Frequenzband (HP 510) beinhaltet die Detailinformationen für entsprechende Kanten. Hier hat sich die Anzahl der horizontalen Pixel halbiert.

Es werden zuerst alle Zeilen des Originalbildes zu einem eindimensionalen Signal zusammengefasst. Dieses wird mittels Filterbank in zwei Frequenzbänder geteilt. Das untere Frequenzband (Signal am Ausgang des TP 509) zeigt ein Bild, dessen vertikale Kanten gegenüber dem Originalbild unschärfer dargestellt sind, das obere Frequenzband ((HP 510) beinhaltet die Detailinformationen für entsprechende Kanten. Aufgrund der Unterabtastung hat sich die Anzahl der vertikalen Pixel halbiert.

Filterung der Zeilen (horizontale Filterung) PC

Es werden zuerst alle Spalten des Originalbildes zu einem eindimensionalen Signal zusammengefasst. Dieses wird mittels Filterbank in zwei Frequenzbänder geteilt. Das untere Frequenzband (Signal am Ausgang des TP 509) zeigt ein Bild, dessen horizontalen Kanten gegenüber dem Originalbild unschärfer dargestellt sind, das obere Frequenzband ((HP 510) beinhaltet die Detailinformationen für entsprechende Kanten. Aufgrund der Unterabtastung hat sich die Anzahl der horizontalen Pixel halbiert.

Filterung der Spalten (vertikale Filterung) PDA_Phone

Es werden die Spalten zu einem eindimensionalen Signal zusammengefasst, und in zwei Frequenzbänder geteilt. Das untere Frequenzband (TP 509) zeigt ein Bild, dessen horizontale Kanten gegenüber dem Originalbild unschärfer dargestellt sind, das obere Frequenzband ((HP 510) beinhaltet die Detailinformationen für entsprechende Kanten. Hier hat sich die Anzahl der horizontalen Pixel halbiert.

Es werden zuerst alle Zeilen des Originalbildes zu einem eindimensionalen Signal zusammengefasst. Dieses wird mittels Filterbank in zwei Frequenzbänder geteilt. Das untere Frequenzband (Signal am Ausgang des TP 509) zeigt ein Bild, dessen vertikale Kanten gegenüber dem Originalbild unschärfer dargestellt sind, das obere Frequenzband (HP 510) beinhaltet die Detailinformationen für entsprechende Kanten. Aufgrund der Unterabtastung hat sich die Anzahl der vertikalen Pixel halbiert.

Filterung der Zeilen (horizontale Filterung) PDA_Phone

Es werden zuerst alle Spalten des Originalbildes zu einem eindimensionalen Signal zusammengefasst. Dieses wird mittels Filterbank in zwei Frequenzbänder geteilt. Das untere Frequenzband (Signal am Ausgang des TP 509) zeigt ein Bild, dessen horizontalen Kanten gegenüber dem Originalbild unschärfer dargestellt sind, das obere Frequenzband (HP 510) beinhaltet die Detailinformationen für entsprechende Kanten. Aufgrund der Unterabtastung hat sich die Anzahl der horizontalen Pixel halbiert.

Filterbank der Wavelettransformation

1

Filterbank versus Wavelettransformation

• diskrete Wavelettransformation entspricht einer im Aufbau genau festgelegten Filterbank

Filterbank einer diskreten Wavelettransformation PC

Filterbank einer diskreten Wavelettransformation PDA_Phone

Inverse Wavelettransformation PC

Inverse Wavelettransformation PDA_Phone

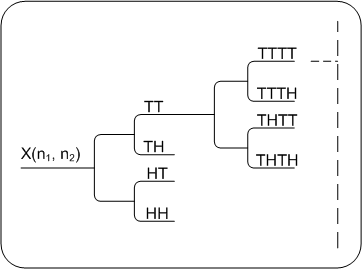
2

Filterbank versus Wavelettransformation

Die diskrete Wavelettransformation entspricht einer im Aufbau genau festgelegten Filterbank. Die Abbildung zeigt Arbeitsweise der von der zweidimensionalen (diskreten) Wavelettransformation verwendeten Filterbank. Man sieht, es handelt sich dabei um eine Kaskadenschaltung von Filterbanken, die jeweils zwei Frequenzbänder erzeugen.

Filterbank einer diskreten Wavelettransformation PC

• x(n1,n2) ist das zweidimensionale Bild
• In einer ersten Stufe wird das Zeilensignal des Bildes in ein unteres und in ein oberes Frequenzband aufgeteilt.
• Das obere Frequenzband wird dann spaltenmäßig in ein HP und in ein TP Frequenzband geteilt ( in Zeichnung HT H für Zeilensignals, T des Spaltensignals und .HH).
• das untere Frequenzband wird ebenfalls wieder in zwei Frequenzbänder aufgeteilt.. Es ergeben sich daraus die Signale TT und TH
• Die Signale HT, HH und TH sind die ersten Detailsignale des Bildes
• Das Signal TT wird der nächsten Filterstufe zugeführt. Dort werden auf gleiche Weise die nächsten Detailsignale eruiert, das verbleibende TTTT Signal wird an die nächste Filterstufe weiter gegeben.
• Da bei jeder Filterstufe das Signal (sowohl Zeilen wie auch Spalten) mit einem Faktor 2 unterabgetastet wird, liefert jede Stufe ein Bild mit halbierter Auflösung. Das Signal kann nun bis zu einer beliebig kleinen Skalierung gefiltert werden. Die kleinste mögliche Skalierung ist eine Auflösung von einem Pixel.

Filterbank einer diskreten Wavelettransformation PDA_Phone

• x(n1,n2) ist das zweidimensionale Bild
• In einer ersten Stufe wird das Zeilensignal des Bildes in ein unteres und in ein oberes Frequenzband aufgeteilt.
• Das obere Frequenzband wird dann spaltenmäßig in ein HP und in ein TP Frequenzband geteilt ( in Zeichnung HT H für Zeilensignals, T des Spaltensignals und .HH).
• das untere Frequenzband wird ebenfalls wieder in zwei Frequenzbänder aufgeteilt.. Es ergeben sich daraus die Signale TT und TH
• Die Signale HT, HH und TH sind die ersten Detailsignale des Bildes
• Das Signal TT wird der nächsten Filterstufe zugeführt. Dort werden auf gleiche Weise die nächsten Detailsignale eruiert, das verbleibende TTTT Signal wird an die nächste Filterstufe weiter gegeben.
• Da bei jeder Filterstufe das Signal (sowohl Zeilen wie auch Spalten) mit einem Faktor 2 unterabgetastet wird, liefert jede Stufe ein Bild mit halbierter Auflösung. Das Signal kann nun bis zu einer beliebig kleinen Skalierung gefiltert werden. Die kleinste mögliche Skalierung ist eine Auflösung von einem Pixel.

Inverse Wavelettransformation PC

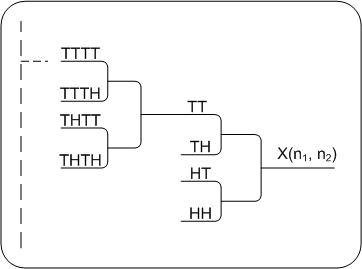
Die inverse Transformation setzt das Originalbild aus dem Bild mit geringster Skalierung und den Detailinformationen wieder zusammen.

Inverse Wavelettransformation PDA_Phone

Die inverse Transformation setzt das Originalbild aus dem Bild mit geringster Skalierung und den Detailinformationen wieder zusammen.

Bildliche Darstellung der Wavelettransformation bovi2000 kana2004

1

Bildliche Darstellung der Wavelettransformation bovi2000 kana2004

• Ausgang Filterbank
  • Bild mit geringster Auflösung
  • Detailinformationen für jede Stufe

Darstellung der Filterstufen bei der WavelettransformationPC

Darstellung der Filterstufen bei der Wavelettransformation PDA_Phone

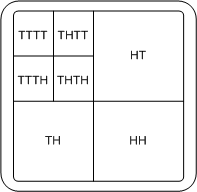
2

Bildliche Darstellung der Wavelettransformation bovi2000 kana2004

Als Ergebnis liefert die Filterbank der Wavelettransformation das Bild mit geringster Auflösung und die Detailsignale, mit deren Hilfe man das Originalbild wieder rekonstruieren kann. Wie wir gesehen haben, bleibt die Gesamtdatenmenge trotz Mehrfachauflösung auf Grund der Unterabtastung konstant. So kann man alle Bildinformationen, die die Wavelttransformation liefert, in einem einzigen Bild repräsentieren. Die Bildgröße ist dabei gleich der Bildgröße des Originalbildes.

Darstellung der Filterstufen bei der Wavelettransformation PC

Die Abbildung zeigt die Position der Filterausgänge in der bildlichen Darstellung. In der bildlichen Darstellung sieht man an hand des Bildbeispiels Lena die Informationen, die die unterschiedlichen Filterstufen beinhalten.

• TH zeigt Detailinformationen von vertikal verlaufenden Kanten
• HT zeigt Detailinformationen von horizontal verlaufenden Kanten
• HH zeigt Detailinformationen von diagonal verlaufenden Kanten

Darstellung der Filterstufen bei der Wavelettransformation PDA_Phone

Die Abbildung zeigt die Position der Filterausgänge in der bildlichen Darstellung. In der bildlichen Darstellung sieht man an hand des Bildbeispiels Lena die Informationen, die die unterschiedlichen Filterstufen beinhalten.

• TH zeigt Detailinformationen von vertikal verlaufenden Kanten
• HT zeigt Detailinformationen von horizontal verlaufenden kanten
• HH zeigt Detailinformationen von diagonal verlaufenden Kanten

Wavelettransformation mit verschiedenen Mutterwavelets kana2004

1

Haar-versus Daubechies Wavelet PC

Waveletzerlegung mit Haar-Wavelets

Waveletzerlegung mit Daubechies-Wavelets

Haar-versus Daubechies Wavelet PDA_Phone

Waveletzerlegung mit Haar-Wavelets

Waveletzerlegung mit Daubechies-Wavelets

Applet: Waveletkomposition applet42003

Online Alternative

2

Unterschiedliche Mutterwavelets

Bilder von kana2004 Wie bereits erwähnt, handelt es sich bei den Bildern, die die Wavelettransformation repräsentieren, nicht einfach um unterabgetastete Bilder, sondern ihre Pixelwerte stellen die Waveletkoeffizienten dar. Mit Hilfe dieser Koeffizienten und den Wavelets kann aus einem Bild geringerer Skalierung (Auflösung) das Originalbild approximiert werden. Ist die Qualität der Approximation gut, so werden die Detailinformationen weniger werden, die diese Informationen repräsentierenden Bilder werden weniger Strukturen haben. Die erzielbare Qualität der Approximation hängt dabei entscheidend von den verwendeten Wavelets ab. Die optimalen Wavelets sollten das Originalbild möglichst fehlerfrei rekonstruieren können.

Haar-versus Daubechies Wavelet PC

Waveletzerlegung mit Haar-Wavelets

Waveletzerlegung mit Daubechies-Wavelets

Es wird die Transformation mit Haar Wavelets und die mit Daubechies Wavelets miteinander verglichen. Man sieht, dass bei der Haartransformation in den Bildern für Detailinformationen noch ein relativ hoher Informationsgehalt steckt. Im Vergleich dazu ist dieser bei der Daubechie Wavelets viel geringer. Daraus folgt, dass die Bildapproximation mittels Daubechie Wavelets bedeutend besser ist. Für Bildkodierungen werden daher meist Daubechie-Wavelets verwendet.

Haar-versus Daubechies Wavelet PDA_Phone

Waveletzerlegung mit Haar-Wavelets

Waveletzerlegung mit Daubechies-Wavelets

Es wird die Transformation mit Haar Wavelets und die mit Daubechies Wavelets miteinander verglichen. Man sieht, dass bei der Haartransformation in den Bildern für Detailinformationen noch ein relativ hoher Informationsgehalt steckt. Im Vergleich dazu ist dieser bei der Daubechie Wavelets viel geringer. Daraus folgt, dass die Bildapproximation mittels Daubechie Wavelets bedeutend besser ist. Für Bildkodierungen werden daher meist Daubechie-Wavelets verwendet.

Applet:Waveletkomposition applet42003

Beschreibung

Man hat die Möglichkeit aus 3 vorgegebenen Bildern auszuwählen. Weiters wichtig ist die Option, welche Kompression angewendet werden soll: Haar oder Daubecies (N=3). Letztere braucht im Vergleich länger bei der Ausgabe.

Nachdem man auf den "wavelet"-Button gedrückt hat, wird das ausgewählte Bild in 4 Gruppen unterteilt, in Tieffrequenzbereich und Hochfrequenzbereich in Richtung der x-Achse, in Richtung der y-Achse, und in Richtung der xy-Achse.

Durch weiters Klicken auf den "wavelet"-Button wird jeweils das Bild im Tieffrequenzbereich in weitere Bereich aufgespalten.

Instruktionen

Zuerst hat man die Möglichkeit oben auf der Buttonleiste zwischen 3 Bildern auszuwählen. Nach Belieben darf man sich zwischen "Lenna", "Otoha" und "Yasu" entscheiden. Weiters ist ein Pull-down Menü zu finden, hier gibt es 2 Wavelets zur Auswahl.

Klickt man nun auf den Button "Wavelet", erscheint im rechten Kästchen das Ergebnis der Transformation. Wenn der "Wavelet"-Button weiter gedrückt wird, wird jeweils der Niederfrequenzbereich des Bildes (links oben - "low-freq. components) transformiert.

Online Alternative

3

Links auf zum Thema passendem Applet

Applet42001: Fractional Spline Wavelet Transform

• Kurzbeschreibung
  • User hat die Möglichkeit sich eines der angebotenen Bilder oder ein eigenes Bild vom Desktop zu wählen. Man kann nun das Bild transformieren, indem man die gegebenen Faktoren verändert, dabei verändern sich auch die Graphen der Funktionen, „scaling function“ und „wavelet function“. Neben dem unten abgebildeten Originalbild wird das transformierte Bild ausgegeben
• Autor
  • Daniel Sage – Biomedical Imaging Group - daniel.sage@epfl.ch
• www
  • http://bigwww.epfl.ch/demo/fractsplines/demoprep.html

Applet40407: Wavelet Image Coder

• Kurzbeschreibung
  • Ein Bild wird in seine „Bestandteile“, seine Koeffizienten herausgefiltert und angezeigt, und das Bild wird wieder zusammengesetzt wiedergegeben.
• Autor
  • Laurent Balmelli
• www
  • http://www.andrew.cmu.edu/user/jelenak/Teaching/Applets/2DWavelet/ImageCoder.html

Mehrfachauflösung zur Bildkompression

1

Kompression durch Kodierung von Bild mit geringerer Auflösung

• Jede Filterstufe halbiert Auflösung des Bildes
  • Halbierung der Auflösung Entspricht jeweils eine Datenreduktion um Faktor 4
  • Jedes Bild entspicht einem Kompressionsfaktor
  • Oiginalbild kann durch Bild geringerer Auflösung approximiert werden
• Nachteil
  • hohe Frequenzkomponenten werden vollständig aus Bild entfernt

Perzeptuelle Kodierung

• Prinzip JPEG Bildkodierung
• Hohe Frequenzen von menschlichem Auge weniger genau wahrgenommen
• Hohe Frequenzen werden mit kleineren Wortlängen kodiert
• Jedem Subband wird ein Quantisierungsfaktor zugeordnet
• Effekt
  • sehr hohe Anzahl an Waveletkoeffizienten, die hohe Frequenzen repräsentieren
  • kleine Veringerung der Wortlänge ergibt hohe Datenreduktion
  • Wavelet aus diesem Grund der DCTrobert link auf Anker LU19: DCT legen überlegen

Entropiekodierung

• Kodierungstechniken wie JPEG2000 im verlustlosen Modus (siehe JPEG2000 Kodierungstechnk)

Applet 42004:

2

Es gibt nun verschiedenste Möglichkeiten, die Mehrfachauflösung der Wavelettransformation zur Kompression von Bilddaten zu nutzen.

Kompression durch Kodierung von Bild mit geringerer Auflösung

Jede Filterstufe liefert ein Bild mit der halben Auflösung des vorhergehenden Bildes. Das entspricht einer Pixelreduktion (und somit Datenreduktion) um einen Faktor 4. Wählt man nun zum Beispiel das Bild aus der dritten Filterstufe, und erzeugt damit mit Hilfe der Wavelets eine Approximation des Originalbildes, erreicht man einen Kompressionsfaktor von 1:64. Die Qualität des so entstandenen Bildes hängt dabei stark von den verwendeten Wavelets ab. Es gehen durch diese äußerst simple Technik allerdings alle hochfrequenten Bildinformationen verloren.

Perzeptuelle Kodierung

Ähnlich wie bei der JPEG Bildkodierung mittels Quantisierungstabellen können die Frequenzkoeffizienten unterschiedlich bewertet werden. Das menschliche Auge ist für hohe Frequenzwerte weniger empfindlich. So können diese Werte mit einer geringeren Wortlänge kodiert werden. Es wird dabei jedem Subband (jedes Subband steht für eine bestimmte Frequenz) ein unter perzeptuellen Aspekten gewählter Quantisierungsfaktor zugeordnet. Aus der bildlichen Darstellung der Wavelettransformation sieht man, dass je höher die Frequenz ist, umso mehr Koeffizienten sind zu deren Repräsentation vorhanden. Somit bringt auch nur eine kleine Verkürzung der Wortlänge dieser Werte bereits einen großen Beitrag zur Datenkompression (Durch diese Eigenschaft ist die Wavelettransformation der DCT 242 in Bezug auf Kompression haushoch überlegen).

Entropiekodierung

Kodierungstechniken wie JPEG2000 im verlustlosen Modus (siehe JPEG2000 Kodierungstechnk) können Datenkompression durch reine Entropiekodierung erzielen.

Waveletkompression applet42004

Beschreibung

Man hat die Möglichkeit aus 3 vorgegebenen Bildern auszuwählen. Weiters ist die Option wichtig, welche Kompression angewendet werden soll: Haar, Daubecies (N=3) und Daubecies (N=5).

Nachdem man auf den "wavelet"-Button gedrückt hat, wird das ausgewählte Bild in 4 Gruppen unterteilt, in Tieffrequenzbereich und Hochfrequenzbereich in Richtung der x-Achse, in Richtung der y-Achse, und in Richtung der xy-Achse.

Durch weiters Klicken auf den "wavelet"-Button wird jeweils das Bild im Tieffrequenzbereich in weitere Bereiche aufgespalten

Instruktionen

Zuerst hat man die Möglichkeit oben auf der Button Leiste zwischen 3 Bildern auszuwählen. Nach Belieben darf man sich zwischen "Lenna", "Otoha" und "Yasu" entscheiden. Weiters ist ein Pull-down Menü zu finden, hier gibt es 3 Wavelets zur Auswahl.

• Klickt man nun auf den Button "Wavelet", erscheint im rechten oberen Kästchen das Ergebnis der Transformation.
• Wie bereits oben erklärt, zeigt das Bild, welches sich links unten befindet, die quantisierten Wavelet-Koeffizienten, welche nur 7 Werte (0, +-sigma, +-2sigma, +-3sigma) einnehmen können.
• Wenn der "Wavelet"-Button weitergedrückt wird, wird jeweils der Niederfrequenzbereich des Bildes (links oben - "low-freq. components) transformiert.
• Mit dem "compress"-Button gelangt man zum komprimierten Ergebnis des Ausgangsbilds, welches im rechten unteren Bild ausgegeben wird.

Online Alternative

Zusammenfassung Waveletbasierte Bildkodierung

1

Waveletbasierte Bildkodierung

• Kern von JPEG2000
• Teil von MPEG-4
• Mehrfachauflösung
• Filterbank
• Mehrfachauflösung zur Bilddatenkompression

2

Waveletbasierte Bildkodierung

Die waveletbasierte Bildkodierung wird in der nächsten Zeit immer mehr an Bedeutung gewinnen, da sie den Kern des JPEG2000 Standards darstellt. Auch in Teilen des MPEG-4 Standards wird sie beschrieben. Was die Wavelets für die Datenkompression so interessant macht, ist, dass sie das Bild in mehrere Auflösungenstufen unterteilt, ohne dass eine zusätzliche Datenmenge anfällt. Die Bilder geringer Auflösung entstehen dabei nicht durch eine Unterabtastung der Bildpunkte, sondern ihre Bildpunkte sind die Waveletkoeffizienten. Mit deren Hilfe kann das Originalbild aus einem Bild geringer Auflösung approximiert werden. die Qualität der Approximation ist dabei stark von der verwendeten Mutterwavelet abhängig. Die Differenz zwischen approximierten Bild und Originalbild ist in den Subbands gespeichert. Die diskrete Wavelettransformation ist ident mit einer Filterbank, bei der pro Stufe das Signal in 2 Frequenzbänder aufgeteilt wird.Die Mehrfachauflösung ist für die Datenkompression von so großer Bedeutung, da nur eine geringe Anzahl an Koeffizienten die tiefen Frequenzen repräsentieren, eine sehr hohe Anzahl die hohen Frequenzen. daraus folgt, nur eine geringe Reduktion der Wortlänge der hohen Frequenzen bringt eine erhebliche Datenreduktion.

3

Hintergrundinformation zum Testbild "Lena" wiki2001

Lena - Testbild für Bildkodierung

Lena (auch Lenna) ist eines der meistverbreiteten Testbilder in der digitalen Bildbearbeitung. Es kommt zum Einsatz, wann immer die Funktionsweise eines Algorithmus demonstriert wird, z.B. in Lehrbüchern oder Folienvorträgen. In diesem Zuge hat Lena in Informatikerkreisen einen gewissen Kultstatus erreicht. Das Bild eignet sich unter anderem deshalb so gut als Testobjekt, weil es gleichermaßen aus großen, einfachen Flächen und Flächen mit vielen Details besteht.

Lena - Testbild für Bildkodierung PC lena1972-2

Lena - Testbild für Bildkodierung PDA_Phone lena1972-2

Das Originalbild

Das ursprüngliche Lena-Bild stammt aus der Ausgabe des Männermagazins Playboy von November 1972. Es zeigt das schwedische Playmate Lena Sjööblom (vom Playboy "Lenna" genannt). Das Original des als Testbild verwendeten Ausschnitts liegt in der Bilder-Datenbank des Signal & Image Processing Institute der University of Southern California (USA). Es misst 512 x 512 Pixel und hat eine Größe von 768 kB.

Abbildung: Lena Original PC lena1972-1

Abbildung: Lena Original PDA_Phone lena1972-1

Lena Sjööblom

Über die dargestellte Lena Sjööblom ist bekannt, dass sie am 31. März 1951 in Schweden geboren wurde, 1988 durch den Journalisten einer Computerzeitschrift von der Zweckentfremdung ihres Fotos erfuhr und 1997 zum 50. Geburtstag der Konferenz der Society for Imaging Science and Technology eingeladen wurde, wo sie Autogramme gab und für Erinnerungsfotos zur Verfügung stand. Sie ist verheiratet und hat drei Kinder.