Einleitung watk2001-1,138 poul1999,10-1

1

Einleitung

• Bezeichnung - Wavelet ist engliche Übersetzung von Ondelette (kleines gewelltes Kopfhaar)
• Motivation - Analyse instationärer Signale mit hoher Bandbreite und steilen Signalanstiegen
• Vorteil - Originalbereich und transformierter Bereich nicht absolut voneinander getrennt
  • Originalbereich - Zeit oder Ort
  • transformierter Bereich - Zeit (oder Ort) und Skalierung

2

Einleitung

Die Wavelettransformation ist ein mathematisches Werkzeug, das in der Mitte der 80ger Jahre entwickelt wurde. Die grundlegenden Arbeiten daran wurden von einer Gruppe französischer Mathematiker geleistet. So war auch der ursprüngliche Name „Ondelette“ (französisch: kleines gewelltes Kopfhaar)watk2001-1. Bei der Übersetzung ins Englische entstand dann die heute allgemein gebräuchliche Bezeichnung „Wavelet“ (englisch: Wellchen). Die Wavelet Transformation ist optimiert auf die Analyse von instationären Signalen mit einem breiten Frequenzspektrum und steilen Signalanstiegen. Sie basiert auf der Short-time Fouriertransformation, die wiederum eine spezielle Form der Fouriertransformation ist. Bei der Wavelettransformation konnten die Nachteile der STFT 498 eliminiert werden. Das Hauptaugenmerk wird bei der Wavelettransformation auf den Zeitbereich (bzw. Ortsbereich) gelegt. Bei der Transformation wird das Originalsignal nicht in einen vom Originalbereich absolut abgegrenzten Frequenzbereich transformiert, sondern in eine Darstellungsform übergeführt, die Information von Zeit (oder Ort) und Skalierung (entspricht der Frequenz) beinhaltet.

Wavelet Transformation watk2001-1

1

auto

Wavelettransformation basiert auf STFT 498

Basisfunktionen

• Es werden prinzipiell nur Signalabschnitte untersucht
• Basisfunktionen - keine harmonischen Schwingungen, sondern "Wavelets" mit endlicher Ausdehnung
• Jede Transformation hat Mutterwavelet
• Eigenliche Wavelets leiten sich von Mutterwavelet ab
  • Skalierung
  • Verschiebung

Variable Fensterlänge

2

auto

Die Wavelet Transformation basiert auf der Short Time Fouriertransformation. Durch die Verwendung alternativer Basisfunktionen und einer mit der Frequenz variablen Fensterlänge beseitigt sie die Nachteile der Short Time Fouriertransformation.

Grundeigenschaften der Wavelettransformation

Basisfunktionen

• Die Wavelettransformation bezieht sich schon vom Prinzip her ausschließlich auf die Analyse von Fenstern eines Signals (=Signalabschnitten)
• Als Basisfunktionen dienen keine harmonische Schwingungen, sondern Funktionen mit endlicher Ausdehnung. Diese Basisfunktionen werden als „Wavelets“ (=Wellchen) bezeichnet.
• Für eine Transformation wird eine für die Anwendung geeignete Mutterwavelet ausgewählt. Die verschiedenen Wavelets, aus denen die Funktion aufgebaut wird, unterscheiden sich von der Mutterwavelet nur durch Skalierung und Verschiebung

Variable Fensterlänge

Bei der STFT 498 Fouriertransformation wird das Signal im Originalbereich in Fenster eingeteilt. Die Fensterlänge ist für jeden Signalabschnitt und für jede Frequenz gleich. Für jedes Fenster wird dann das Frequenzspektrum berechnet. Bei der Wavelettransformation ist die Länge des Fensters davon abhängig, auf welche Frequenz das Signal hin untersucht wird. Untersucht man das Signal auf dessen tiefen Frequenzen, wird das Signal in große Fensterlängen unterteilt, für hohe Frequenzen hingegen in kleine Fensterlängen

• Hohe Frequenzen, das entspricht in Bildern scharfe Kanten, in Audiosignalen plötzliche Anstiege der Lautstärke, werden mit kurzen Basisfunktionen (entspricht kurzem Fenster) transformiert. Dadurch ist gewährleistet, dass hohe Frequenzkomponenten dem Ereignis im Originalbereich sehr genau zugeordnet werden können.
• Für tiefe Frequenzen wird eine längere Fensterlänge gewählt, Dadurch ergibt sich eine hohe Frequenzauflösung.

Basisfunktionen der Wavelet Transformation

1

FT -Harmonische Schwingungen

• Basisfunktionen - Sinus und Kosinusschwingungen mit unendlicher Ausbreitung
• dadurch sich ergebender Nachteil - Eine bestimmte Frequenz kann keinem bestimmten Punkt im Original zugewiesen werden

WT - Mutter Wavelets

• Basisfunktionen -sind Ableitungen von einer Mutterwavelet, haben endliche Ausdehnung
• sich dadurch ergebender Vorteil - eine bestimmte Frequenz kann einem bestimmten Punkt im Original zugewiesen werden

Galerie von Mutter - Wavelets PC

Haar wavelet

:

Daubechies 4 wavelet

Daubechie18 wavelet

Galerie von Mutter - Wavelets PDA_Phone

Haar wavelet

:

Daubechies 4 wavelet

Daubechie18 wavelet

Wavelets

• Wavelets ergeben sich aus Mutterwavelet
• Analoges harmonischen Schwingung/Wavelets
  • Basisfunktionen harmonische Schwingungen unterscheiden sich durch unterschiedliche Frequenz
  • Wavelets unterscheiden sich durch unterschiedliche Skalierung (analog zur Frequenz) und Verschiebung

Zusammenhang Skalierung und Frequenz/Signaldauer

• ...keine Skalierung
• ...Dehnung des Mutterwavelets
• ...Stauchung des Mutterwavelets

Abbildung: Stauchung eines Mutterwavelets PC

Abbildung: Stauchung eines Mutterwavelets PDA_Phone

Abbildung: Verschiebung eines Mutterwavelet PC

Abbildung: Verschiebung eines Mutterwavelet PDA_Phone

2

FT -Harmonische Schwingungen

Bei der Fouriertransformation sind die Basisfunktionen Sinus- und Kosinussignale, die im Unendlichen beginnen, und im Unendlichen enden. Im transformierten Bereich (Frequenzbereich) sind die entsprechenden Amplituden der Basisfunktionen angegeben. Aus der unendlichen Ausdehnung der Basisfunktionen ergibt sich der Nachteil, dass die Frequenzkomponenten keinem bestimmten Zeitpunkt (bzw einem Ort) im Originalbereich zugewiesen werden können.

WT - Mutter Wavelets

Um die Nachteile von harmonischen Schwingungen als Basisfunktionen zu eliminieren, dienen bei der Wavelet Transformation Funktionen mit endlicher Ausdehnung als Basisfunktionen. Diese Basisfunktionen werden als Mutter-Wavelets bezeichnet.

Galerie von Mutter - Wavelet PC clem2000

Je nach Anwendung gibt es verschiedene Formen von Mutter Wavelets. Zu beachten ist, dass es sich bei Wavelets immer um Funktionen im Originalbereich handelt.

Haar wavelet

:

Daubechies 4 wavelet

Daubechie18 wavelet

Galerie von Mutter - Wavelets PDA_Phone clem2000

Haar wavelet

:

Daubechies 4 wavelet

Daubechie18 wavelet

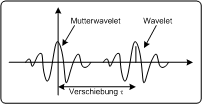
Wavelets

Aus einem Mutter Wavelet ergeben sich die eigentlichen Wavelets, aus welchen ein beliebiges Signal aufgebaut werden kann. Wie harmonische Schwingungen verschiedene Frequenzen haben können, können Wavelets verschiedene Skalierungen und Verschiebungen haben. Die Skalierung entspricht der Frequenz, die Verschiebung gibt Aufschluss, wann (bzw wo) ein bestimmtes Wavelet in Erscheinung tritt.

Zusammenhang Skalierung und Frequenz/Signaldauer

Durch die Skalierung wird das Mutter Wavelet gestaucht beziehungsweise gedehnt. Mathematisch beschrieben wird die Skalierung durch den Skalierungsfaktor s. dabei gilt:

• ...keine Skalierung
• ...Dehnung des Mutterwavelets
• ...Stauchung des Mutterwavelets

Wie in der Abbildung ersichtlich, wird durch die Stauchung des Mutterwavelet ein Wavelet erzeugt, das zwar die gleiche Form hat, aber von kürzerer Dauer ist und eine höhere Frequenz aufweist.

Abbildung: Stauchung eines Mutterwavelets PC

Abbildung: Stauchung eines Mutterwavelets PDA_Phone

Abbildung: Stauchung eines Mutterwavelets

Skalierung einer Daubechie 18 Mutterwavelet watk2001-1, 142. Mitte: Mutterwavelet, links: Wavelet duch Dehnung des Mutterwavelets rechts. Wavelet durch Stauchung des Mutterwavelets

Umgekehrt entsteht durch Dehnungein Wavelet, das von längerer Dauer und niederer Frequenz gegenüber der Mutterwavelet ist.

Zusammenhang Zeit(bzw Ort)/Verschiebung

Da im Gegensatz zu harmonischen Schwingungen Wavelets eine endliche Ausdehnung haben, muss auch angegeben werden, zu welchem Zeitpunkt beziehungsweise an welchem Ort ein Waveletsignal liegt. Das Mutterwavelet liegt immer im Nullpunkt des Koordinatensystems. Der Verschiebungsfaktor gibt die Position des Wavelets bezüglich der Position des Mutterwavelets an.

Abbildung: Verschiebung eines Mutterwavelet PC

Abbildung: Verschiebung eines Mutterwavelet PDA_Phone

Wavelet Koeffizienten

1

Vergleich FT und WT Koeffizienten

• Fouriertransformation
  • Frequenzkoeffizienten geben an, mit welcher Intensität eine harmonische Schwingung bestimmter Frequenz in einem Signal vorhanden ist
• Wavelettransformation
  • Wavelet Koeffizienten gebenan, mit welcher Intensität ein Wavelet bestimmter Skalierung und Verschiebung in einem Signal vorhanden ist

Frequenz und WT Koeffizienten

• WT 499 Koeffizienten für hoheFrequenzen
  • sehr stark bei steilen Signaländerungen
  • hochfrequente Wavelets nur von kurzer Dauer
  • Koeffizienten gut der Position im Originalsignal zuordbar
• WT 499 Koeffizienten fürt iefe Frequenzen
  • entspricht gleichmäßigem Signalsverlauf
  • tieffrequente Wavelets von langer Dauer
  • Großer Bereich im Original kann mit nur sehr wenigen Koeffizienten beschrieben werden

2

Vergleich FT und WT Koeffizienten

So wie bei der Fouriertransformation ein Signal aus harmonischen Schwingungen mit unterschiedlichen Frequenzen aufgebaut wird, wird bei der Wavelettransformation das Originalsignal durch Wavelets unterschiedlicher Verschiebungs- und Skalierungsfaktoren zusammengesetzt. Bei der Fouriertransformation geben die Frequenzkoeffizienten an, mit welcher Intensität eine harmonische Schwingung bestimmter Frequenz in einem Signal vorhanden ist. Äquivalent dazu geben Wavelet Koeffizienten an, mit welcher Intensität ein Wavelet bestimmter Skalierung und Verschiebung in einem Signal vorhanden ist. Die Waveletkoeffizienten sind also eine Funktion der Skalierung s und der Verschiebung τ.

Frequenz und WT Koeffizienten

Hohe Frequenzen

An Signalsprüngen erreichen Beträge jener Waveletskoeffizienten besonders hohe Werte, die hohe Frequenzen repräsentieren. Durch das Prinzip der Skalierung sind diese hochfrequenten Wavelets besonders von kurzer Dauer, das heißt, es können solche Waveletkoeffizienten (und somit Frequenzen) einer Position im Originalsignal sehr genau zugeordnet werden.

Tiefe Frequenzen

Der tieffrequente Teil des Signals wird durch Wavelets mit tiefer Frequenz und daher langer Dauer repräsentiert. Das entspricht einem langem Fenster. Das lange Fenster liefert eine feine Frequenzauflösung.

3

Applet: Wavelet Koeffizienten applet40406

Kurzbeschreibung

Dieses Applet funtioniert wie eine “Wavelet-Transformation-Maschine”. Man kann sein eigenes Signal laden, indem man eines aus dem Menü auswählt. Die Wavelet-Transformation des ausgewählten Signals wird erstellt. Weiters kann man die Koeffizienten abspeichern und später die „inverse“-Transformation durchzuführen.

Diskrete Wavelet Transformation poul1999

1

Diskrete WT für kontinuierliche Funktionen

• Wavelettransformation
  • kontinuierliches Originalsignal
  • kontinuierliche Skalierungsfunktion
• Diskrete Wavelettransformation
  • kontinuierliches Originalsignal
  • diskrete Skalierungsfunktion

Diskrete WT für diskrete Funktionen

• disktretes Originalsignal - ebenfalls diskrete Skalierungsfunktion und diskreter Zeitverlauf (Verschiebung)

2

Diskrete WT für kontinuierliche Funktionen

Bisher wurde von Wavelttransformationen gesprochen, mit deren Hilfe ein beliebíges Signal in Wavelets zerlegt wird, die im Bezug auf Skalierung und Verschiebung beliebig variieren können. Daraus ergibt sich unmittelbar, dass die Funktion der Waveletkoeffizienten eine kontinuierliche Funktion ist. Für viele Anwendungen besteht allerdings der Wunsch, ein Signal mit möglichst wenigen Parametern darstellen zu können. Daraus entwickelte sich die Diskrete Wavelettransformation (DWT).

Diskrete Wavelettransformation poul1999, 100-22

Bei einer diskreten Wavelettransformation wird ein beliebiges, also auch ein kontinuierliches Signal, durch Wavelets mit diskreten Skalierungs- und Verschiebungswerten dargestellt. Die zweidimensionale Funktion wird zu einer Diskreten Funktion. Der Term „Diskret“ in der DWT bezieht sich also ausschließlich auf den Transformierten Bereich.

Formel

	Waveletkoeffizient für das Wavelet mit der Skalierung und der Verschiebung
	Wavelet mit der Skalierung und der Verschiebung
	Eine von der Funktion unabhängige Konstante

Aus der Formel lässt sich leicht erkennen, dass sowohl die Originalfunktion wie auch die Wavelets kontinuierliche Funktionen sind. Diskret ist ausschließlich die Waveletkoeffizientenfunktion .

Diskrete WT für diskrete Funktionen

Bei multimedialen Daten (Audio- und Bildsignale) ist die Originalfunktion ebenfalls eine diskrete Funktion. Die Waveletkoeffizienten errechnen sich mit den gleichen Algorithmen, die, wie oben beschrieben, für kontinuierliche Funktionen verwendet werden.

DWT und Datenkompression

1

Abbildung: Verschiebungs/Skalierungsgitter für DWTpoul1999 PC

Abbildung: Verschiebungs/Skalierungsgitter für DWTpoul1999 PDA_Phone

Abbildung: Verschiebungs/Skalierungsgitter für DWTpoul1999

Ein Punkt entspricht Position eines möglichen Wavelet-Koeffizienten

Wavelets für Datenkompression

• Anzahl der Werte im diskreten Originalsignal = Anzahl der Koeffizienten
  • Tieffrequenter Anteil - wird mit sehr wenigen Koffizienten dargestellt
  • hochfrequenter Anteil - wird mit sehr vielen Koeffizienten dargestellt
• Hauptanteil multimedialer Daten meist im tiefen Frequenzbereich
  • mit wenigen Koeffizienten großer Teil des Signals darstellbar
  • Nur kleine Änderung der Wortlänge der Koeffizienten für hohe Frequenzen bewirkt hohe Datenreduktion

2

Aus der Theorie der Wavelets lässt sich ableiten, welche diskreten Skalierungs- und Verschiebungswerte von Wavelets vorhanden sein müssen, um den eindeutigen Aufbau eines beliebigen Originalsignals zu ermöglichen.

Abbildung: Verschiebungs/Skalierungsgitter für DWT poul1999 PC

Abbildung: Verschiebungs/Skalierungsgitter für DWTpoul1999 PDA_Phone

Abbildung: Verschiebungs/Skalierungsgitter für DWTpoul1999

Jeder Punkt entspricht einem Wavelet mit entsprechender Verschiebungs und Skalierung. Jedes beliebige Signal lässt sich mittels DWT in diese Wavelets zerlegen beziehungsweise mit diesen Wavelets mittels inverser DWT wieder eindeutig aufbauen. (Die Skalierung ist hier zwecks besserer Übersicht in einem logarithmischen Maß eingezeichnet, da die möglichen Skalierfaktoren sich aus einer exponentiellen Funktion ergeben).

Verschiebungs/Skalierungsgitter

Die oberste Reihe entspricht den höchstfrequenten Wavelets mit kürzester Ausdehnung. Man sieht, dass diese Wavelets in sehr kurzen Zeitabständen vorhanden sind. Für eine Signalanalyse repräsentieren sie steile Signaländerungen in sehr hoher zeitlicher (für Bilddaten örtlicher) Auflösung. So werden auch im transformierten Bereich eng aneinander liegende Signalspitzen des Originalsignals getrennt von einander aufgelöst. Mit zunehmender Skalierung (Frequenzen der Wavelets werden niedriger, die Ausdehnung wird größer) wird die zeitliche (bzw örtliche) Auflösung geringer. Für die Signalanalyse bedeutet das, dass das Signal in diesem Frequenzbereich mit nur sehr wenigen Koeffizienten dargestellt werden kann.

Wavelets für Datenkompression

Durch obige Abbildung kann man langsam erahnen, was die DWT für die verschiedenen Algorithmen zur Datenkompression so interessant macht. Bei den meisten Bild- und Audiosignalen liegt der Hauptanteil des Signals in den tieferen Frequenzbereichen. Diese werden in der DWT durch sehr wenige Koeffizienten repräsentiert, was gut für eine Datenkompression ist. Signalspitzen (scharfe Kanten in Bilder, plötzliche Änderung der Lautstärke in Audiosignale) werden durch sehr viel mehr Koeffizienten repräsentiert, obwohl sie nur einen verhältnismäßigen geringen Anteil des Gesamtsignals enthalten. Werden nun zum Beispiel hochfrequente Koeffizienten mit einer geringeren Quantisierungsgenauigkeit kodiert, erreicht man durch deren hohe Anzahl eine beträchtliche Datenreduktion.

3

Applet: Wavelets für Datenkompression applet40407

Kurzbeschreibung

• Allgemein besteht die „wavelet based lossy compression
• Transform: die Daten warden zuerst in einen Wavelet –Bereich transformiert. Dieser Schritt ist umkehrbar.
• Quantization: die Wavelet-Koeffizienten warden zu einem bestimmten Alphabet quantisiert. Dieser Schritt ist nicht umkehrbar.  „quantization noise”
• Entropy Coding: die resultierenden Symbole nach der Quantisation warden noch “entropy”-codiert, um die bit-Rate zu reduzieren. Dieser Schritt ist ebenfalls umkehrbar

Multiresolution Signalanalyse

1

Mulitresolution Signalanalyse

• Tieffrequente Wavelets zeigen Signal in geringer Auflösung
• werden die Wavelets der nächsten Skalierstufe zugefügt wird Auflösung erhöht
• Werden alle Koeffizienten zum Signalaufbau verwendet erhält man Originalauflösung

Abbildung: Beispiel Audiosignal poul1999 PC

Abbildung: Beispiel Audiosignal poul1999 PDA_Phone

Abbildung: Beispiel Bildsignal bovi2000 PC

Abbildung: Beispiel Bildsignal bovi2000 PDA_Phone

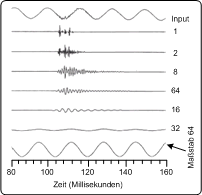
2

Multiresolution Signalanalyse

Es gibt eine Analogie zwischen Waveletanalyse und einem Mikroskop. Die Skalierung korrespondiert dabei mit der Größe der Auflösung des Mikroskops, die Verschiebung mit einer Stelle des Objektes, das man untersuchen will. Wählt man die größtmögliche Skalierung, wird das Bild in kleiner Auflösung dargestellt. Werden jetzt schrittweise die Wavelets mit geringerer Skalierung hinzugefügt, werden die Details mehr und mehr sichtbar, das entspricht einer schrittweisen Erhöhung der Auflösung des Mikroskops. Die Wavelets mit der größtmöglichen Skalierung stellen das Bild in einer geringen Auflösung dar, Die Wavelets der nächsten Skalierungsstufe liefern die Informationen, um das Bild in einer doppelt so hohen Auflösung darstellen zu können. Die übernächste liefert wieder dazu die Differenzwerte, mit deren Hilfe man auf die nächst höhere Auflösungsstufe gelangt, und so fort. Daraus sieht man, dass bei der Wavelettransformation das Signal in verschiedenen Auflösungsstufen dargestellt wird. Es gibt viele Verfahren, die Signale in mehrere Auflösungen aufteilen, was aber die Wavlettransformation so besonders macht, ist, dass trotz der Mehrfachdarstellung eines Signals die Datenmenge gleich bleibt.

Abbildung: Beispiel Audiosignal poul1999 PC

Abbildung: Beispiel Audiosignal poul1999 PDA_Phone

Abbildung: Beispiel Audiosignal poul1999

Oben sieht man das Originalsignal, es handelt sich um einen Sinuston, der zu einem bestimmten Zeitpunkt von einer hochfrequenten Störung überlagert ist. Die geringste Auflösung des Signals ist bei einer Skalierung von 64, hier sieht man zwar das gesamte Originalsignal, Informationen über das zeitlich beschränkte Störsignal sind in dieser Auflösung noch nicht sichtbar. Mit stetig abnehmender Skalierung werden immer mehr Detailinformationen des Störsignals sichtbar.

Beispiel Bildsignal bovi2000 PC

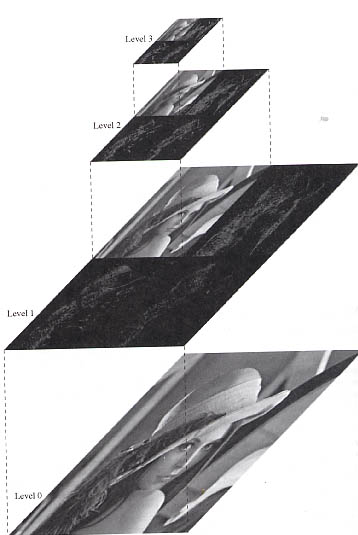
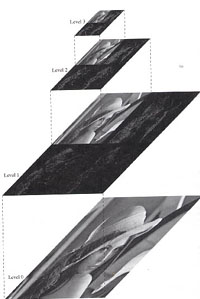
Level 3 stellt das Bild in seiner geringsten Auflösung dar. Mit Hilfe der Wavelets der nächsten Skalierungsstufe gelangt man auf Level 2 der Darstellung. Hier ist das Bild mit einer doppelt so hohen Auflösung dargestellt. So fährt man fort, bis man auf den Level 0, das ist die Darstellung des Bildes in seiner Originalauflösung, gelangt.

Beispiel Bildsignal bovi2000 PDA_Phone

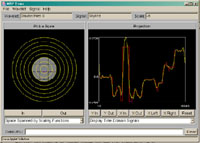
Level 3 stellt das Bild in seiner geringsten Auflösung dar. Mit Hilfe der Wavelets der nächsten Skalierungsstufe gelangt man auf Level 2 der Darstellung. Hier ist das Bild mit einer doppelt so hohen Auflösung dargestellt. So fährt man fort, bis man auf den Level 0, das ist die Darstellung des Bildes in seiner Originalauflösung, gelangt.

3

Applet: Mulitresolution Signalanalyse applet40404

Kurzbeschreibung

Dieses Applet zeigt die Wavelet-basierte Multiresolution Analyse. In linkem Fenster kann man in der Kreisskala mittels der Maus beliebig Kreisflächen markieren. Die Projektion in dieser Kreisfläche wird als gelber Graph dargestellt. Das Originalsignal wird rot angezeigt.

Zusammenfassung

1

• optimales mathematisches Werkzeug
  • instationäre Signale
  • große Bandbreite
  • steile Signalanstiege
• Basisfunktionen
  • Wavelets
    • endliche Ausdehnung
    • je kleiner Ausdehnung,umso höher dieFrequenz
• Vorteile für Datenkompression
  • hohe Frequenzkomponenten können sehr genau lokalisiert werden
  • tiefer Frequenzbereich kann mit sehr wenigen Koeffizienten dargestellt werden

2

Zusammenfassung

Die Motivation zur Entwicklung der Wavelettransformation war, ein mathematisches Werkzeug zu entwickeln, welches optimal zur Analyse von instationären Signalen mit einem hohen Frequenzspektrum und steilen Signalanstiegen zu verwenden ist. Sie baut auf der Fouriertransformation auf, beseitigt aber dessen Nachteile, indem sie nicht in zwei völlig voneinander getrennten Räumen arbeitet, sondern dass im transformierten Raum neben der Frequenz (=Skalierung) auch die Variabel Zeit (bzw. Ort) mit einbezogen wird. So können Frequenzkomponenten direkt einer Position im Originalsignal zugeordnet werden. Diese Eigenschaft wird dadurch erreicht, dass anstatt harmonischer Schwingungen mit unendlicher Ausdehnung Wavelets mit endlicher Ausdehnung verwendet werden. Jedes Wavelet steht dabei für eine bestimmte Frequenz an einem bestimmten Ort (bzw. Zeit). Bei der Disketen Wavelettransformation können Wavelets nur mehr diskrete Skalierungswerte annehmen. Jeder Skalierungswert entspricht dabei einer Auflösungsstufe. Die Verteilung der Koeffizienten ist so, dass nur wenige Koeffizienten für die tiefen Frequenzen stehen, eine sehr hohe Anzahl hingegen für hohe Frequenzen. Diese Eigenschaft der Wavelettransformation ermöglich eine äußert effektive Datenkomprimierung.

3

Zur Lerneinheit passende Links

• http://nt.eit.uni-kl.de/wavelet/ Wavelettutorial der Universiät Karlsruhe
• Index-wavelet Uni-Salzburg ...sbg.ac.at
• wavelet.org
• Wavelet Tutorial-Folien von christopoulos ......homepage; link von jpg.org
• Tutorial-Wavelet+JPEG2000 .....standford.edu
• Introduction to Wavelets Paper von Amara Grap ....amara.com; link von Salzburgindex; Text: gute einführung;
• Amara Grap waveletindex mit abstracts

Zur Lerneinheit passende Applets

Applet 40401

Kurzbeschreibung

Das Applet soll den Graph der skalierten Funktion oder des Wavelets zeigen, welcher im Bereich [0,3] liegt. Mittels der Buttons am unteren Bildschirmrand kann der User vordefinierte Graphen anzeigen lassen, weiters kann man dann den Graphen manipulieren, in dem man in der Funktion den blauen Punkt des Wavelets (bzw den roten Punkt der skalierten Funktion) im Bereich der Parameter „Odd“ und „Even“ bewegt.

Auto(en)

wim@lucent.com

www

http://cm.bell-labs.com/who/wim/cascade/

Applet

Kurzbeschreibung

Dieses applet zeigt zwei skalierte recursive Gleichungen in einer wiederholenden Sequenz. Es zeigt folgende 3 Schritte:

1. Shifting: Die “shift”-Versionen der komprimiert-skalierten Funktionen sind grün dargestellt.
2. Weighting: Die “weighted”-Versionen der “shift” und komprimiert-skalierten Funktionen sind blau dargestellt. The weighted versions of the shifted and compressed scaling functions are shown in blue.
3. Summing: Die Summe von “weighted”-Versionen der “shift” und komprimiert-skalierten Funktionen sind gelb dargestellt. (Zum Schluß bekommt man die skalierte Funktion oder das Wavelet.)

Auto(en)

Haitao Guo

www

http://www-dsp.rice.edu/software/EDU/twoscale.shtml

Applet 40403

Kurzbeschreibung

Dieses Applet zeigt die Parameterisation der skalierten Koeffizienten. In einem Feld von –Pi bis +Pi kann man in linkem Fenster mit der Maus sich beliebig im Feld bewegen. Durch das Fadenkreuz werden 2Parameter angewählt, welche in rechtem Fenster als Wavelet(gelbe Linie) und/ oder skalierte Funktion(rote Linie) angezeigt/ geändert werden. (Die Parameter und skalierte Koeffizienten werden im oberen Textbereich angezeigt.

Auto(en)

Haitao Guo

www

http://www-dsp.rice.edu/software/EDU/wavelet246.shtml

Applet 40405

Kurzbeschreibung

Dieses Applet zeigt das “denoising via thresholding” von Wavelet Koeffizienten. Zuerst wählt man ein Signal und ein Wavelet aus. Das „noisy“-Signal wird im rechten Fenster dargestellt, links die Wavelet-Koeffizienten des „noisy“-Signals. Im linken Fenster kann man das „thresholding“ einstellen, es erscheinen 2 grüne Linien, welche die positiven und negativen Werte des „thresholding“ zeigen. Das „denoised“-Signal wird mit dem eingestellten „thresholding“ im rechten Fenster als gelber Graph dargestellt. Weiters wird das „noise-free“-Signal mit blauen Linien und das „noisy“-Signal mit roten Linien dargestellt.

Auto(en)

Haitao Guo

www

http://www-dsp.rice.edu/software/EDU/denoise.shtml