Motivation

1

Warum digitales Audio?

• Ursprünglich ausschließlich analoges Audio immer mehr von digitalem Audio verdrängt
• Digitales Audio vielfältiger einsetzbar als analoges

Vorteile Digital versus Analog

• Anpassung an Übertragungsbandbreite
• DAB 364
• Audioretrieval
• Hifi 503 Qualität
• Editierbarkeit

2

Warum digitales Audio?

Um Musik, menschliche Stimmen oder allgemeine akustische Ereignisse über Nachrichtenkanäle übertragen beziehungsweise auf Speichermedien archivieren zu können, bedarf es einer geeigneten Aufbereitung akustischer Information. Die ursprünglich analoge Aufbereitungsform wird immer mehr und mehr von der digitalen Audiotechnik abgelöst. Neben qualitativen Aspekten liegt ein Hauptgrund dafür in der Vielfalt, mit welcher ein Signal in digitaler Form kodiert werden kann. So kann ein Signal dem jeweils zur Verfügung stehenden Übertragungs- beziehungsweise Speichermedium durch geeignete Kodierung optimal angepasst werden.

Digital versus Analog

Folgende Beispiele sollen einige Vorteile zeigen, die digitales Audio gegenüber analogem Audio bringt

• Anpassung an Übertragungskanalbandbreite
  • Musik kann in Echtzeit zum Beispiel ohne nennenswerte hörbare Qualitätsverluste über Telefonleitungen übertragen werden, deren Bandbreite für analoge Audiosignale nur den alt bekannten Telefonklang zulassen. Formate wie MP3, AAC und AC-3 wären mit analogen Audiosignalen nicht möglich.
• DAB 364 (Digital Audio Broadcasting) Es können im gleichen Sendegebiet mehr Radiosender empfangen werden, als dies mit analogen Sendern möglich ist. Weiters kann jeder Radiosender zusätzliche Informationen (wie Texte etc) mit dem Signal senden.
• Audioretrievalsollte link auf ../../m05/units/03_21.xml sein - Signalanalysen, wie sie zum Beispiel für Sprach- und Musikerkennungssysteme nötig sind, sind nur mit digital kodiertem Audio möglich
• Hifi 503 Qualität – die Qualität von digitalem Audio übertrifft jene von analogem Audio. Grund dafür sind unter anderem geringeres Rauschen und verzerrungsärmere Wiedergabe.
• Editierbarkeit – Bei analogen Signalen verschlechtert sich die Qualität bei jedem Editierschritt (Mischen mehrerer Quellen, Kopieren etc). Für digitales Audio bleibt die Qualität unverändert.

Analog/Digital Konverter

1

Grundsätzliches

• Analoges Audio
  • Mikrofon wandelt Luftdruckschwankungen in elektrisches Signal
  • Signalverlauf analog den Luftdruckschwankungen
  • Mikrofone können immer nur analoges Signal erzeugen
• Digitales Audio
  • Mikrofon wandelt Luftdruckschwankungen in analoges elektrisches Signal
  • Analog/Digital Wandler - anloger Signalverlauf wird digital kodiert

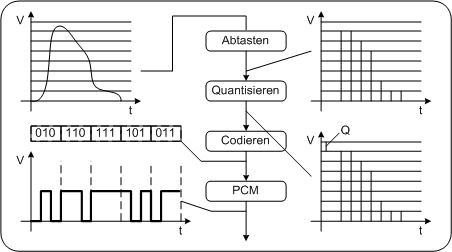
Abbildung: Überblick Analog/Digital Wandlung PC

Abbildung: Überblick Analog/Digital Wandlung PDA_Phone

2

Grundsätzliches

Ausgangspunkt jeder elektronischen Repräsentation akustischer Ereignisse ist immer das Mikrofon. Es wandelt eine Schallwelle in ein elektrisches Signal.

Die Schallwelle erzeugt Luftdruckschwankungen an der Membran des Mikrofons. Die Bewegung der Membran wird in ein elektrisches Signal gewandelt. Der Spannungsverlauf des elektrischen Signals ist dabei analog den zeitlichen Luftdruckschwankungen an der Membran. Mikrofone können allerdings nur analoge Signale erzeugen. Zur digitalen Repräsentation muss ein so genannter Analog/Digital Konverter erst das analoge in ein digitales Signal wandeln.

Abbildung: Überblick Analog/Digital Wandlung PC

Abbildung: Überblick Analog/Digital Wandlung PDA_Phone

Abbildung: Überblick Analog/Digital Wandlung PDA_Phone

Am Eingang liegt das analoge elektrische Audiosignal. Durch Abtasten ergeben sich zeitlich diskrete Werte, die Quantisierung ordnet jedem dieser Werte einen diskreten Amplitudenwert zu. Diese werden dann anschließend binär kodiert. Das PCM Signal schließlich ist die binäre Amplituden/Zeitdarstellung des Signals.

Abtasten

1

Prinzip

• Analoges Signal wird in diskreten Zeitabständen abgetastet und gespeichert (sample and hold)
• Zeitabstände so gewählt, dass durch Abtasten kein Informationsverlust
• Nyquist-Shannon Theorem bestimmt den maximal erlaubten Zeitabstand zwischen zwei diskreten Werten

Nyquist-Shannon Theorem

Welche Abtastfrequenz für welches Signal?

• Hohen Abtastfrequenz
  • hohe Bandbreite
  • effektive Reduktion von Aliasfrequenzen
  • hohe Datenarate
• Geringe Abtastfrequenz
  • geringe Datenrate

Begriffserklärungen

Aliasfrequenz

Wenn Abtastfrequenz niedriger als Nyqistfrequenz Entstehung von Fremdfrequenzkomponenten (=Aliasfrequenzen)

Bandbreite

Hörbeispiel Abtastfrequenz

Datenrate

Datenrate = Abtastfrequenz x Wortlänge (/Abtastwert)

2

Prinzip

Das analoge Signal ist immer eine kontinuierliche Funktion der Zeit. Zeitkontinuierliche Signale können aber nicht digital verarbeitet werden, sondern nur Signale mit zeitdiskreten Werten. Beim Abtasten wird in gleichmäßigen Zeitabständen der momentane Amplitudenwert des kontinuierlichen Zeitsignals gemessen und gespeichert (englisch: Sample and Hold). Die Zeitabstände müssen so gewählt werden, dass durch die Diskretisierung keine Information verloren geht, d.h. dass ein digital/analog Konverter mit Hilfe der Abtastwerte die analoge Funktion originalgetreu rekonstruieren kann. Wie oft ein analoges Signal abgetastet werden muss, ohne dabei Informationen zu verlieren, wird durch das Nyquist-Shannon Theorem festgelegt.

Nyquist-Shannon Theorem

Ein abgetastetes Signal lässt sich nur dann wieder hinreichend ohne Informationsverlust rekonstruieren, wenn gilt:

	Abtastfrequenz. Sie gibt an, wie oft das analoge Signal pro Sekunde abgetastet wird
	Ist die höchste im analogen Signal vorkommende Frequenz

Abtastung eines Audiosignals

Es soll ein Audiosignal so digitalisiert werden, dass keine der hörbaren Frequenzkomponenten verloren gehen. Die für unser Ohr gerade noch hörbare Frequenz ist um die 20kHz. Es muss daher mindestens eine Abtastfrequenz von 40kHz gewählt werden.

Welche Abtastfrequenz für welches Signal?

Bei der Festlegung einer geeigneten Abtastfrequenz muss zwischen den Merkmalen Aliasfrequenzen, Bandbreite und Datenrate abgewogen werden. Generell gilt:

• Für die Wahl einer möglichst hohen Abtastfrequenz spricht die hohe Bandbreite und eine effektive Reduktion von Aliasfrequenzen
• Für die Wahl einer möglichst niedrigen Abtastfrequenz spricht eine reduzierte Datenmenge

Aliasfrequenz

Das Nyquist-Shannon Theorem geht davon aus, dass oberhalb der Maximalfrequenz des analogen Signals wirklich alle Frequenzkomponenten Null sind. In der Praxis aber sind die Frequenzkomponenten, die knapp oberhalb der Maximalfrequenz liegen, zwar stark gedämpft, aber eben nicht absolut Null. Diese Frequenzen erzeugen durch deren Spiegelung an der Abtastfrequenz neue Fremdfrequenzkomponenten, die so genannten Aliasfrequenzen, die unterhalb der Maximalfrequenz liegen. Bei Audiosignalen sind Aliasfrequenzen als zusätzliche Töne hörbar, die im Originalsignal nicht vorhanden waren. Bei der Festlegung der geeigneten Abtastfrequenz wird daher für viele Anwendungen meist ein höherer als der vom Nyquist-Shannon Theorem geforderte Mindestwert gewählt.

Applet: Aliasfrequenz applet40802

Beschreibung

Unter "Aliasing" ("Verfremdung") versteht man die Verfälschung von Bildern oder anderen analogen Informationen bei der Digitalisierung und digitalen Verarbeitung mit einer zu geringen Abtastrate.

Die bekannteste Form des Aliasing ist der Moiré-Effekt. Um korrekte und wiederholbare Ergebnisse zu erzielen, muß z.B. jedes Bild mit einer Abtastrate digitalisiert werden, die mindestens doppelt so groß ist wie die Rasterung der Vorlage.

Beispielsweise erfordert ein Bild, das mit 150 Linien pro Zoll gerastert ist, einen Scanner der mindestens eine Abtastrate von 300 dpi (Punkte pro Zoll) senkrecht zu den Linien im Bild realisieren kann. Die Abtastrate gibt die Häufigkeit an, mit der eine Messung in einem bestimmten Zeitraum oder einer räumlichen Dimension durchgeführt wird. Üblicherweise wird so eine Abtastrate bei Scanner oder Sound-Digitalisierung angegeben.

Die Anwendung zeigt grafisch wie ein untergesampelt-sinusförmiges Signal erscheint. In Bezug auf die Sampling-Theorie kann ein sinusförmiges Signal aus Werte rekonstruiert werden, welche aus diskreten und gleichen Intervallen gesampelt wurden, vorausgesetzt dass die Signalfrequenz weniger als die halbe gesampelte Frequenz ist. Jegliche Komponenten eines gesampelten Signals mit einer Frequenz über dieser Grenzschwelle, werden meist "Folding Frequency" genannt und bezieht sich auf "Aliasing" bzw "Verfremdung".

Diese Anwendung basiert auf einer fixen Samplingrate von 8000 samples pro Sekunde (1 Sample alle .0125 Millisekunden). Die folding frequency beträgt dann die Hälfte von 8000 Hz oder 4000Hz.

Instruktionen

Die Eingangsfrequenz wird in Hertz in das Textkästchen eingetragen. Wenn "Input Signal" angewählt ist und dann der "Plot"-Button betätigt wird, wird das Signal graphisch dargestellt. Mit Hilfe der "Grid"-Checkbox können vertikale Grenzlinien, wo das Signal gesampelt ist, ein- und ausgeblendet werden. "Sample Points" zeigen die gesampelten Werte des Eingangssignals, und können ebenfalls zu- und ausgeschalten werden. Weiters gibt es noch die "Alias Frequency"-Checkbox, welche nur sichtbar ist, wenn die Eingangsfrequenz über 4000 Hz Folding Frequency liegt. Diese Checkbox kontrolliert die bereits dargestellte Grafik eines sinusförmigen Signals.

Also at http://www.dsptutor.freeuk.com/aliasing/AliasingDemo.html

Bandbreite

Als Bandbreite eines Signals versteht man die Differenz zwischen der im Signal vorkommenden höchsten und tiefsten Frequenz. Aus dem Nyquist-Shannon Theorem sieht man, dass ein enger Zusammenhang zwischen Abtastfrequenz und Bandbreite besteht. Will man ein Signal mit hoher Bandbreite übertragen, muss eine entsprechend hohe Abtastfrequenz gewählt werden.

auto

Beispiele zur Veranschaulichung des Zusammenhanges Abtastfrequenz und Bandbreite

Datenrate

Die Datenrate ergibt sich aus:

Datenrate = Abtastfrequenz x Wortlänge (/Abtastwert)

Eine hohe Abtastrate bringt also eine hohe Datenrate mit sich.

Wie groß ist die Datenrate des Signals (=Stereosignal) einer Audio-CD?

Wortlänge/Abtastwert = 16bit

Abtastfrequenz = 44.1kHz

3

Link auf Applet Aliasfrequenz

Link: http://www.dsptutor.freeuk.com/aliasing/AliasingDemo.html

Applet: Aliasfrequenz applet40802

Beschreibung

Unter "Aliasing" ("Verfremdung") versteht man die Verfälschung von Bildern oder anderen analogen Informationen bei der Digitalisierung und digitalen Verarbeitung mit einer zu geringen Abtastrate.

Die bekannteste Form des Aliasing ist der Moiré-Effekt. Um korrekte und wiederholbare Ergebnisse zu erzielen, muß z.B. jedes Bild mit einer Abtastrate digitalisiert werden, die mindestens doppelt so groß ist wie die Rasterung der Vorlage.

Beispielsweise erfordert ein Bild, das mit 150 Linien pro Zoll gerastert ist, einen Scanner der mindestens eine Abtastrate von 300 dpi (Punkte pro Zoll) senkrecht zu den Linien im Bild realisieren kann. Die Abtastrate gibt die Häufigkeit an, mit der eine Messung in einem bestimmten Zeitraum oder einer räumlichen Dimension durchgeführt wird. Üblicherweise wird so eine Abtastrate bei Scanner oder Sound-Digitalisierung angegeben.

Die Anwendung zeigt grafisch wie ein untergesampelt-sinusförmiges Signal erscheint. In Bezug auf die Sampling-Theorie kann ein sinusförmiges Signal aus Werte rekonstruiert werden, welche aus diskreten und gleichen Intervallen gesampelt wurden, vorausgesetzt dass die Signalfrequenz weniger als die halbe gesampelte Frequenz ist. Jegliche Komponenten eines gesampelten Signals mit einer Frequenz über dieser Grenzschwelle, werden meist "Folding Frequency" genannt und bezieht sich auf "Aliasing" bzw "Verfremdung".

Diese Anwendung basiert auf einer fixen Samplingrate von 8000 samples pro Sekunde (1 Sample alle .0125 Millisekunden). Die folding frequency beträgt dann die Hälfte von 8000 Hz oder 4000Hz.

Instruktionen

Die Eingangsfrequenz wird in Hertz in das Textkästchen eingetragen. Wenn "Input Signal" angewählt ist und dann der "Plot"-Button betätigt wird, wird das Signal graphisch dargestellt. Mit Hilfe der "Grid"-Checkbox können vertikale Grenzlinien, wo das Signal gesampelt ist, ein- und ausgeblendet werden. "Sample Points" zeigen die gesampelten Werte des Eingangssignals, und können ebenfalls zu- und ausgeschalten werden. Weiters gibt es noch die "Alias Frequency"-Checkbox, welche nur sichtbar ist, wenn die Eingangsfrequenz über 4000 Hz Folding Frequency liegt. Diese Checkbox kontrolliert die bereits dargestellte Grafik eines sinusförmigen Signals.

Also at http://www.dsptutor.freeuk.com/aliasing/AliasingDemo.html

Quantisierung

1

Prinzip

• Quantisierung
• Analoger Betrag der Werte werden digitalen Kodwörtern zugeordnet
• Anzahl der Bitstellen bestimmt die Anzahl der möglichen Kodwörter
• 

AudioCD

16 Bit Wortlänge

65536 Kodwörter

Welche Wortlänge für welches Signal?

• Je größer Wortlänge, umso geringer der Quantisierungsfehler
• Je kürzer Wortlänge, um so kleiner die Datenmenge

Quantisierungsrauschen

• Analoge Amplitudenwerte können beliebige Werte annehmen
• Digitale Werte nur diskrete Werte
• Welche diskreten Werte möglich, hängt von Wortlänge ab
• Quantisierungsrauschen
  • Fehler durch Zuordnung analoger auf digitalen Wert
  • 
• Quantisierungsrauschen bei Audio
  • bei 16 Bit Quantisierungsrauschen nicht mehr hörbar

Wahl der geeigneten Wortlänge

Quantisierungsfehler als Quantisierungsrauschen hörbar

Audio-CD

• Wortlänge 16bit
  • Quantisierungsrauschen nicht mehr hörbar

Hörbeispiel

Lineare Quantisierung PC

Lineare Quantisierung PC

Nicht lineare Quantisierung PC

Nicht lineare Quantisierung PDA_Phone

Digitale Telefonie tele2002

• Standards
  • A-law (europäischer Standard)
  • u-law (nordamerikanischer Standard)
• nichtlineare Quantisierung (logarithmische Skalierung des Wertebereiches)
  • 8 Bit Wortlänge gleiche Sprachqualität wie 14 Bit linear
  • Bei 8kHz ergibt sich eine Datenrate von 64kBit/s.

MPEG Audio

Nichlineare Quantisierung als Hybridkodierung (siehe Motivation und Überblick) bei MP3

2

Prinzip

Durch die Abtastung werden in regelmäßigen Zeitabständen Amplitudenwerte abgetastet. Um digital weiter verarbeitbar zu sein, müssen auch die Beträge der durch die Abtastung gewonnenen Werte in einer diskreten Form dargestellt werden, d.h. sie müssen quantisiert werden: Es werden dabei den abgetasteten analogen Werten diskrete Zahlenwerte zugeordnet. Wie viel unterschiedliche Zahlenwerte darstellbar sind, hängt von der Wortlänge (Anzahl der Bitstellen) ab, welche man pro Abtastwert zur Verfügung hat. Es gilt:

	Anzahl der mögliche darstellbaren Zahlenwerte
	Anzahl der Bitstellen, die man zur Darstellung eines Abtastwertes zur Verfügung hat.

Audio für Audio-CD

Für Audio-CD wird eine Wortlänge von 16 Bit/Abtastwert verwendet. Mit 16 Bit sind 65536 unterschiedliche Werte darstellbar.

Welche Wortlänge für welches Signal?

Bei der Festlegung einer geeigneten Wortlänge muss zwischen den Merkmalen Quantisierungsrauschen und Datenrate abgewogen werden. Generell gilt:

• Je höher man die Anzahl der Bitstellen (Wortlänge) wählt, umso kleiner wird das Quantisierungsrauschen
• Bei kurzer Wortlänge reduziert sich die Datenmenge

Quantisierungsrauschen

Die analogen Werte können innerhalb eines bestimmten Wertebereiches, der durch den im Signal vorkommenden kleinsten Amplitudenwert (die kleinste vorkommende Lautstärke) und den größten Amplitudenwert (entspricht der größten vorkommenden Lautstärke) begrenzt ist, jeden beliebigen Wert annehmen, diskrete Zahlenwerte hingegen nur jene Werte, die mit den zur Verfügung stehenden Bitstellen darstellbar sind. Bei der Quantisierung wird dem analogen Abtastwert der ihm am nächst gelegene diskrete Wert zugeordnet. Es kommt daher bei der Quantisierung immer zu einem Fehler, den so genannten Quantisierungsfehler. Der Quantisierungsfehler errechnet sich wie folgt:

	Quantisierungsfehler für einen Abtastwert
	Quantum oder Quantisierungsintervall: Abstand zwischen zwei nebeneinanderliegende diskrete Zahlenwerte

Wahl der geeigneten Wortlänge

Bei Wiedergabe des Audisignals wird der Quantisierungsfehler als Quantisierungsrauschen (siehe auch Grundlagen der perzeptuellen Audiokodierung) hörbar. Aus der Gleichung sieht man, dass gilt:

Je größer die Wortlänge, umso kleiner das Quantisierungsintervall und umso kleiner der Quantisierungsfehler. Große Wortlängen produzieren somit nur ein geringes Quantisierungsrauschen.

Audio-CD

Im Standard für Audio-CD hat man die Wortlänge auf 16 Bit festgelegt. Aus empirischer Erfahrung weiß man, dass das durch diesen Wert eingeführte Quantisierungsrauschen für unser Gehör in den meisten Fällen nicht mehr wahrgenommen werden kann.

Lineare Quantisierung PC

Im Allgemeinen sind bei der Quantisierung die Quantisierungsintervalle konstant. Man spricht von einer linearen Quantisierung.

Durch die Quantisierung können Amplitudenwerte nur bestimmte Werte annehmen. Im Allgemeinen liegen die Werte des analogen Signals aber zwischen zwei solcher möglichen Werte. Den Analogenwerten wird bei der Quantisierung der ihnen am nächstliegenden diskreten Wert zugeordnet.

Lineare Quantisierung PDA_Phone

Im Allgemeinen sind bei der Quantisierung die Quantisierungsintervalle konstant. Man spricht von einer linearen Quantisierung.

Durch die Quantisierung können Amplitudenwerte nur bestimmte Werte annehmen. Im Allgemeinen liegen die Werte des analogen Signals aber zwischen zwei solcher möglichen Werte. Den Analogenwerten wird bei der Quantisierung der ihnen am nächstliegenden diskreten Wert zugeordnet.

Nicht lineare Quantisierung

Bei der nichtlinearen Quantisierung hingegen variiert die Größe des Quantisierungsintervalles. Im unteren Wertebereich sind die Intervalle klein, im oberen sind sie groß.

Abbildung: Nicht lineare Quantisierung PC

Abbildung: Nicht lineare Quantisierung PDA_Phone

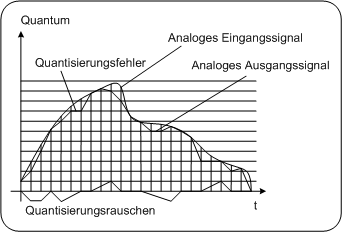
Abbildung: Nicht lineare Quantisierung

Nichtlineare Quantisierung: Die Größe der Quantisierungsintervalle ist nicht über den Gesamtenwertebereich konstant. Kleinere Werte werden feiner aufgelöst, größer Werte werden gröber aufgelöst.

Warum nichtlineare Quantisierung ?

Die Motivation zur nichtlinearen Quantisierung liegt in der Reduktion der Datenrate. Dadurch, dass die Quantisierungsintervalle mit steigender Amplitude immer größer werden, benötigt man geringerer Wortlängen, um die Werte darzustellen. Dass diese Art von Datenreduktion ohne großen Qualitätsverlusten verbunden ist, ist dem Maskierungseffekt aus verdanken (siehe Grundlagen der perzeptuellen Audiokodierung).Aus diesem geht hervor, dass große Amplitudenwerte (größere Lautstärke) ein höheres Maskierungsverhalten gegenüber dem durch die Quantisierung eingeführten Quantisierungsrauschen aufweisen als kleine Amplitudenwerte. Durch die nichtlineare Quantisierung werden kleine Amplitudenwerte sehr fein quantisiert, dementsprechend klein ist daher auch das Quantisierungsrauschen. Große Werte werden gröber quantisiert, dementsprechend groß ist auch das Quantisierungsrauschen, welches aber für unser Ohr nicht wahrnehmbar ist, weil es von der Intensität des Signals maskiert wird.

Die nichtlineare Quantisierung wird hauptsächlich für einfache Kompressionsverfahren verwendet.

Digitale Telefonie tele2002

Audiokodierungsstandard zur digitalen Telefonie:

• A-law (europäischer Standard)
• u-law (nordamerikanischer Standard)

Durch nichtlineare Quantisierung (logarithmische Skalierung des Wertebereiches) wird mit 8 Bit Wortlänge praktisch die gleiche Sprachqualität erreicht, die sich bei Verwendung linearer Quantisierung mit 14 Bit erreichen ließe. Bei der standardisierten Abtastfrequenz von 8kHz ergibt sich eine Datenrate von 64kBit/s.

MPEG Audio

Aber auch bei komplexen Kodierungsalgorithmen findet die nichtlineare Quantisierung als Komponente einer Hybridkodierung (siehe Motivation und Überblick) Verwendung (z.B. MP3).

Darstellungsformen eines Audiosignals

1

Amplituden/Zeit Funktion

Bild

Frequenzspektrum

Bild

Spektrogramm

Bild

2

auto

Es gibt verschiedene Formen, ein Audiosignal zu repräsentieren. Jede Darstellung bietet dabei einen besonderen Aspekt des Signals. Welche Repräsentationsform die günstigste ist, hängt von der jeweiligen Anwendung ab.

Beispiel: Algorithmen zur Datenkompression benötigen meist eine Darstellung des Signals, die dessen Frequenzkomponenten zeigen, Algorithmen wiederum die entscheiden können sollen, ob es sich bei einem Audiosignal um eine Sprachaufnahme oder nicht handelt, benötigen eine Amplituden/Zeit Funktion etc.

Amplituden/Zeit Funktion

Aus dem Amplituden/Zeit Diagramm kann man ablesen, welche Intensität das Signal zu welchem Zeitpunkt hat. Sie ist die ursprünglichste der verschiedenen Repräsentationsformen. Schallwandler (Mikrofone, Lautsprecher) können nur mit dieser Repräsentationsform von Audio arbeiten.

Es fehlt Bild!!!!

Frequenzspektrum

Im Frequenzspektrum wird angezeigt, welche Frequenzen mit welcher Intensität im Audiosignal vorhanden sind. Aus dem Frequenzspektrum kann man allerdings nicht lesen, zu welchem Zeitpunkt entsprechende Frequenz signifikant wird.

Es fehlt Bild!!!!

Vorteile

Aus dem Frequenzspektrum kann man erkennen, welche Bandbreite das Signal hat, ob es sich um ein eher helles oder dumpfes Audiosignal handelt, ob vorwiegend harmonische Anteile vorhanden sind oder ob Geräusche im Gesamtklang dominieren.

Spektrogramm

Diese Darstellungsform ist eine Kombination aus Amplituden/Zeit Diagramm und Frequenzspektrum. Es zeigt an, zu welchem Zeitpunkt welche Frequenzen welche Intensitäten aufweisen. Das Spektrogramm bietet somit die aussagekräftigste bildliche Darstellung eines Audiosignals. Diese komplexe Darstellung macht man sich zum Beispiel in Audioretrievalsysteme (siehe Audioretrieval) zu Nutze.

Es fehlt Bild!!!!

Vorteile

Es sollen Klangdateien auf Ähnlichkeit untersucht werden. Dazu können deren Spektrogramme mit den gleichen Algorithmen untersucht werden, die auch für Imageretrieval robert link auf m5LU8 setzen verwendet werden.