Einleitung watk2001-1,138 poul1999, 10-1 krey1999

1

Geschichtliches und Überblick

• Fouriertransformation - benannt nach Jean-Baptiste Joseph de Fourier (1768-1830)
• Fourierreihe - entwickelt im Jahre 1822 für sein Hauptwerk „Theorie analytique de la chaleur“
• Fourierreihe - für periodische Signale, Originalsignal wird als Summe von Sinus und Cosinusfunktionen dargestellt
• Fourierintegral - wie Fourierreihe, gilt aber für allgemeine, nicht periodische Signale
• Fouriertransformation - komplexe Darstellung des Fourierintegrals
• Frequenzspektrum - wichtig für perzeptueller Datenkompression, erhält man mit Hilfe der Fouriertransfomation

2

Geschichtliches und Überblick

Der französische Mathematiker und Physiker Jean-Baptiste Joseph de Fourier (1768-1830) entwickelte im Jahre 1822 für sein Hauptwerk „Theorie analytique de la chaleur“, in welchem die Theorie zur Wärmeleitung abgehandelt wird, eine neue mathematische Reihe, die Fourierreihe. Es stellte sich bald heraus, dass diese mathematische Reihe zur Analyse verschiedenster physikalischer Beobachtungen geeignet ist. In weiterer Folge übte sie auch einen großen Einfluss auf die Weiterentwicklung der gesamten Mathematik aus. Die Fourierreihe ist nur für periodische Signale gültig, eine Erweiterung davon, das Fourierintegral, lässt die gleichen Algorithmen auch auf nichtperiodische Funktionen anwenden. Die Fouriertransformation schließlich ist die komplexe Form des Fourierintegrals, mit dessen Hilfe man das Frequenzspektrum für jede beliebige Funktion erhält. Das Frequenzspektrum bildet die Basis für verschiedenste Analyse- und Interpretationsmöglichkeiten von Funktionen. So arbeiten auch die meisten Algorithmen zur perzeptuellen Datenkompression im Frequenzspektrum. Einen allgemeinen Überblick über die Fouriertranformation bietet eineLerneinheit im Modul1.

Die Fourierreihe watk2001-1,138 poul1999, 10-1 krey1999

1

Einführung Fourierreihe

• Fourierreihe - periodische Funktionen können als eine unendliche Folge von harmonischen Schwingungen (Kosinus und Sinusschwingungen) dargestellt werden
• Frequenzen der Schwingungen - ganzzahliges Vielfaches des periodischen Signals
• Sinus und/oder Cosinus - hängt von Symetrieeigenschaften der Funktion ab

Fourierreihe für ungeraden periodischen Funktionen

Fourierreihe für gerade periodische Funktionen

Fourierreihe für allgemein periodische Funktionen

Eulersche Formeln

Applet: Fourierreihe applet40306 jar und code vorhanden

Also available at http://www.ims.tuwien.ac.at/%7Emigl/modul4-appletsammlung/40306/index.html

2

Einführung Fourierreihe

Fourier konnte zeigen, dass periodische Funktionen beliebiger Form als eine unendliche Folge von harmonischen Schwingungen (Kosinus und Sinusschwingungen) dargestellt werden können. Die Frequenzen der einzelnen Schwingungen sind dabei ein ganzzahliges vielfaches der Frequenz des periodischen Signals. Mit welchen harmonischen Schwingungen - ob Kosinus oder Sinusschwingungen - eine periodische Funktion aufgebaut werden kann, hängt von dessen Symmetrieeigenschaften ab. Man unterscheidet zwischen ungeraden, geraden und allgemeinen Funktionen.

Fourierreihe für ungeraden periodischen Funktionen

Ungerade Funktion

Eine gerade Funktion ist eine Funktion, die symmetrisch zur y-Achse ist. Eine Funktion heisst gerade, wenn gilt

Fouriersatz

Eine periodische, gerade Funktion beliebiger Form kann als eine unendliche Folge von Kosinusfunktionen dargestellt werden.

mit

...Amplitudenwerte für Sinusschwingungen

...Index der Sinusfunktion

Fourierreihe für gerade periodische Funktionen

Gerade Funktion

Eine gerade Funktion ist eine Funktion, die symmetrisch zur y-Achse ist. Eine Funktion heisst gerade, wenn gilt

Fouriersatz

Eine periodische, gerade Funktion beliebiger Form kann als eine unendliche Folge von Kosinusfunktionen dargestellt werden.

mit

...Amplitudenwerte für Kosinusschwingungen

..Index der Kosinusfunktion

Fourierreihe für allgemein periodische Funktionen

Allgemeine Funktion

Unter allgemein ist hier gemeint, dass die Funktion keinerlei Symmetrieeigenschaften gegenüber der y-Achse aufweist.

Fouriersatz

Eine allgemeine periodische Funktion kann als eine Folge von Sinus- und Cosinusfunktionen dargestellt werden.

Diese mathematische Reihe wird als Fourierreihe bezeichnet, die Koeffizienten als Fourierkoeffizienten. Mit dem Koeffizienten vor dem Summenzeichen ist auch berücksichtigt, dass eine periodische Funktion auch einen Gleichanteil haben kann.

Eulersche Formeln

Die Fourierkoeffizienten errechnen sich aus den Eulerschen Formeln

Applet: Fourierreihe applet40306 jar und code vorhanden

Beschreibung

Periodische Funktionen lassen sich als Überlagerung von sinus- und cosinusförmigen Teilschwingungen erzeugen. Die Anwendung generiert den Klang des Signales in Echtzeit und lässt so einen akustischen Eindruck der Überlagerungen zu.

In den oberen beiden Eingabefeldern können Formeln eingegeben werden. Diese werden durch Drücken auf "Enter" geparst. Die Variable "x" wird dabei jeweils mit den Nummern der Koeffizienten ersetzt.

Darunter können die 13 Teilschwingungen sowohl als sinus- als auch als cosinusförmige Teilfrequenz einzeln manipuliert werden. Das oberste Feld "a0" beschreibt den Offset. Man kann die Werte entweder in den Textfeldern eingeben oder über die Schieberegel inkrementell verändern. Das Drücken des jeweiligen Buttons setzt die Werte wieder zurück.

Die Anwendung speichert bis zu drei Signale gleichzeitig. Zwischen diesen kann mit den Radio-Buttons "Wave 1-3" durchgewechselt werden. So können Auswirkungen auf Veränderungen der Signale sowohl optisch als auch akustisch wahrgenommen und überprüft werden.

Instruktionen

• Um ein Sägezahnsignal zu erstellen, gib im Eingabefeld der sinusförmigen Oszillaton die Formel 1/x ein. Welche Werte nimmt die Variable für die jeweiligen Koeffizienten an?
• Die Formel für das anders orientierte Sägeblattsignal ist (-1^(x-1)). Gib es als neue Wave ein. Wie verhalten sich die Werte gegenüber dem vorigen Signal?
• Stelle die Koeffizienten mit geraden Signalen (b2, b4, ...) nacheinander auf null (Button links neben den Schiebereglern). Wie entwickelt sich das Signal?
• Speichere ein beliebiges Signal in mindestens zwei Wave-Fenstern. Verändere einzelne Komponenten. Wie ändert sich das Signal optisch und akustisch?

Also available at http://www.ims.tuwien.ac.at/%7Emigl/modul4-appletsammlung/40306/index.html

3

Link auf zum Thema passendes Applet

Applet 40308 nur als hyperlink

Kurzbeschreibung

Per Schieberegler können Frequenzanteile verändert werden. Das Signal wird in Echtzeit berechnet.

Autor(en)

Changyeon Won cywon@socrates.berkeley.edu; http://ist-socrates.berkeley.edu/~qiu/pictures/Changyeon.jpg

www

http://socrates.berkeley.edu/~cywon/Indicator.html

Fourierintegral

1

Ableitung von der Fourierreihe

• Reihe - nur gültig für periodische Funktionen
• FourierIntegral - allgemeine Funktionen betrachtet als periodische Funktionen mit unendlicher Periodendauer
• Koeffizienten - Berechnug praktisch unverändert, aber keine Einzelwerte, sondern kontinuierliche Funktion

Fourierintegral

Fourier Kosinusintegral

Fourier Sinusintegral

2

Ableitung von der Fourierreihe

Aus der Fülle an Anwendungsmöglichkeiten der Fourierreihen hat sich nun der Wunsch entwickelt, dass man auch Fourierkoeffizienten für nicht periodische Funktionen berechnen kann. Um diese zu erhalten, bedient man sich eines Tricks: Man interpretiert das nicht periodische Signal als periodisches Signal mit einer unendlich langen Periodendauer. Daraus ergeben sich die Fourierkoeffizienten:

Fourierkoeffizienten für nichtperiodische Funktionen

mit

..Kreisfrequenz

...Frequenz

..Periodendauer

Man sieht, die Algorithmen sind im wesentlichen gleich geblieben, die Periodendauer wurde auf unendlich gesetzt, nur die Fourierkoeffizienten sind keine indizierten Einzelwerte mehr, sondern bilden eine Funktion der Kreisfrequenz w.

Fourierintegral

Aus den Fourierkoeffizienten kann die Funktion mit Hilfe des Fourierintegrals wieder aufgebaut werden:

Diese Formel entspricht im wesentlichen der Fourierreihe für allgemein periodische Funktionen, nur mit dem Unterschied, dass auf Grund der Tatsache, dass die Koeffizienten keine diskreten Werte mehr, sondern Funktionen sind, das Summenzeichen durch ein Integral ersetzt wird.

Fourier Kosinus- und Sinusintegral

Auch nicht periodische Funktionen können gerade oder ungerade Symmetrieeigenschaften bezüglich der y-Achse haben. Aus den Formeln für Fourierkoeffizienten für nichtperiodische Funktionen lässt sich unmittelbar ableiten, dass für diese speziellen Funktionen jeweils ein Teil des Fourierintegrals null wird.

Fourierkosinusintegral

Für gerade Funktionen werden alle b(w) gleich Null. Folglich reduziert sich das Fourierintegral auf

Diese Darstellung bezeichnet man als Fourierkosinusintegral. Eine gerade Funktion wird nur aus Kosinusschwingungen aufgebaut.

Fouriersinusintegral

Für gerade Funktionen werden alle a(w) gleich Null. Folglich reduziert sich das Fourierintegral auf

Diese Darstellung bezeichnet man als Fouriersinusintegral. Eine ungerade Funktion wird nur aus Sinusschwingungen aufgebaut.

Fouriertransformation

1

Komplexe Zahlen

• Ergeben sich aus Lösung der Gleichung "Quadratwurzel aus -1"
• Bestehen aus zwei Teile - Imaginär und Reelen teile
• Ideales Tool für Signalanalyse - Eine Zahl liefert Amplitude und Phasenlage

Fouriertransformation

• Komplexe Dartstellung des Fourierintegrals
• Es werden nicht mehr ein Koeffizient für Sinus uind ein Koeffizient für Kosinus benötigt
• werden durch eine einzige komplexe Zahl ersetzt

Frequenzspektrum

Frequenzspektrum eines Lichtstahles PC

Frequenzspektrum eines Lichtstahles PDA_Phone

Frequenzspektrum mathematischer Funktionen

• Begriff "Spektrum" auch für mathematische Funktionen gebräuchlich
• Fouriertransformation - Berrechnung des Frequenzspektrums
• Im Spektrum werden Intensitäten der Frequenzkomponenten eine Funktion dargestellt
• Frequenzspektrum wird oft bezeichnet als Spektralbereich, Frequenzbereich

Frequenzspektrum periodische/nicht periodische Funktionen

Periodische Funktion PC

Periodische Funktion PDA_Phone

Abbildung: Nicht periodische Funktion PC

Abbildung: Nicht periodische Funktion PDA_Phone

Kosinustransformation

Kosinustransformation für gerade Funktionen

• gerade Funktionen beinhalten nur Kosinusschwingungen
• komplexe Zahl hat nur mehr reelen Teil
• Rechenzeit dadurch halbiert

Kosinustransformation für nicht gerade Funktionen

• Bedingung - Funktion muss endlichen Startpunkt haben, der größer gleich 0 ist
• Kosinustransformation berechnet Spektrum für jene Funktion, die sich aus Original- und dessen Spiegelungum die y-Achse zusammensetzt

Abbildung: Spiegelung von nicht geraden Funktionen PC

Abbildung: Spiegelung von nicht geraden Funktionen PDA_Phone

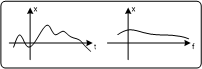
2

Komplexe Zahlen

Die komplexen Zahlen leiten sich aus der Lösung des mathematischen Problems „kann man aus negativen Reelen Zahlen die Quadratwurzel ziehen?“ ab. Komplexe Zahlen bestehen aus zwei Teilen: einem reelen und einem imaginären Teil.

Alle reelen Zahlen sind also eine Teilmenge der komplexen Zahlen, deren Imaginärteile Null sind. In der Funktionsanalyse spielen komplexe Zahlen als ideales Tool eine sehr bedeutende Rolle, da sie neben der Information des Betrages einer Zahl auch die Information eines Winkels haben. Das ist insofern von Bedeutung, da bei Rechnungen mit harmonischen Schwingungen auch immer deren Phasenverschiebungen zueinander zu beachten sind, was zu sehr umständlichen Gleichungen führt. Werden Schwingungen mit Hilfe von komplexen Zahlen dargestellt, beinhalten diese Zahlen bereits die betreffenden Winkelinformationen. Es können so Additionen, Subtraktionen etc auf gewohnt einfacher Art durchgeführt werden, trotzdem werden die Winkelinformationen immer korrekt mitberechnet.

Fouriertransformation

Die Fouriertransformation ist die komplexe Darstellung des Fourierintegrals. Die Fourierkoeffizienten, zwei reele Amplitudenwerte als Funktion der Frequenz (ein Wert steht für die Sinus-, der andere für die Kosinusschwingung) werden durch eine komplexe Zahl, die ebenfalls eine Funktion der Frequenz ist, ersetzt Der Betrag dieser Zahl steht für die Intensität, mit welcher die entsprechende Frequenzkomponente im Signal enthalten ist, der Winkel gibt Information über dessen Phasenlage.

Fouriertransformation

Der Berechnungsalgorithmus, der für eine Funktion eindeutig dessen Frequenzkomponenten berechnet, bezeichnet man als „Fouriertransformation“ bzw. „Fourieranalyse“. Der Algorithmus, der aus den Frequenzkomponenten das Originalsignal rekonstruiert, heißt „ Inverse Fouriertransfomation“.

Frequenzspektrum krey1999

Frequenzspektrum eines Lichtstahls

Der Begriff „Spektrum“ kommt aus der Optik, wo Licht durch Überlagerung von verschiedenen Farben (=Frequenzen) erzeugt wird. Wird das Licht durch ein Prisma in seine Spektralfarben zerlegt, sieht man, welche Farben höhere und welche Farben niedrigere Intensitäten aufweisen. Diese Darstellung des Lichtes bezeichnet man als Frequenzspektrum des Lichtes.

Abbildung: Frequenzspektrum eines Lichtstahles PC

Abbildung: Frequenzspektrum eines Lichtstahles PDA_Phone

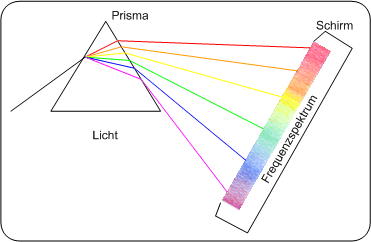
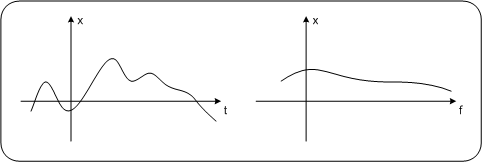
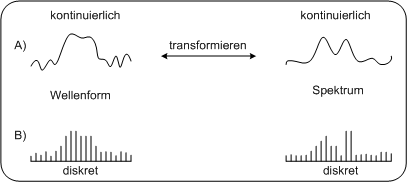
Abbildung: Frequenzspektrum eines Lichtstahles

Das Prisma spaltet den Lichtstrahl in seine Spektralkomponenten auf. Die roten sind die niederfrequenten Komponenten, die blauen die hochfrequenten. Die Intensitätsverteilung als Funktion der Frequenz bezeichnet man als Frequenzspektrum des Lichtstrahls.

Das Prisma erfüllt hier genau die Funktion der Fouriertransformation. In einem umgekehrten Prozess kann durch Bündelung aller Frequenzkomponenten der ursprüngliche Lichtstrahl wieder zusammengesetzt werden. Dieser Prozess entspricht der inversen Fouriertransformation.

Frequenzspektrum mathematischer Funktionen

Der Begriff Frequenzspektrum wird auch bei allgemeinen Funktionen verwendet. Mittels Fouriertransformation erhält man das Frequenzspektrum einer Funktion. Es ist die Darstellung der Intensitäten der Frequenzkomponenten als Funktion der Frequenz. Das Frequenzspektrum wird auch oft als „Spektralbereich“ oder „Frequenzbereich“ eines Signals bezeichnet.

Frequenzspektrum periodischer/nichtperiodische Funktionen

Abbildung:Periodische Funktion PC

Abbildung:Periodische Funktion PDA_Phone

Abbildung:Periodische Funktion

Eine kontinuierliche Periodische Funktion besitzt ein diskretes Frequenzspektrum. Die Frequenzen sind dabei ein ganzzahliges Vielfaches der Grundfrequenz

Abbildung: Nicht periodische Funktion PC

Abbildung: Nicht periodische Funktion PDA_Phone

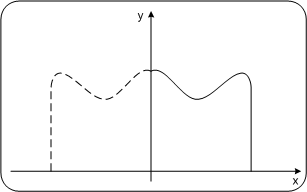
Abbildung: Nicht periodische Funktion

Eine nichtperiodische Funktion besitzt ein kontinuierliches Spektrum

Kosinustransformation

Für gerade Funktionen wird die Funktion durch das Fourierintegral ausschließlich in Kosinusschwingungen aufgelöst. Das bedeutet für dessen komplexe Darstellung, der Fouriertransformation, dass die komplexen Zahlen nur mehr einen Realteil haben, der Imaginärteil aber überall Null ist. Das ist unmittelbar einsichtig, da reine Kosinusschwingungen zu einander keine Phasenverschiebungen haben können. Die Fouriertransformation geht in diesem Fall in die Kosinustransformation über. Der Vorteil der Kosinustransformation besteht darin, dass nur mehr ein Term berechnet werden muss, also nur die halbe Rechenzeit erforderlich ist. In der Datenkomprimierung ist sie vor allem durch den JPEG Standard als Diskrete Kosinustransformation (DCT) und durch die MPEG 31 /Audio Standards (MP3, AAC) in Form einer Modifizierten Diskreten Kosinustransformation (MDCT) praktisch allgegenwärtig.

Kosinustransformation für nicht gerade Funktionen

Funktionen, die in Bild und Audiodaten enthalten sind, sind Funktionen mit endlicher Dauer. Sie haben einen Anfangs- und einen Endpunkt. Legt man den Anfangspunkt in den Koordinaten Nullpunkt, so berechnet die Kosinustransformation das Frequenzspektrum der durch Spiegelung entstandenen geraden Funktion. Auf die Originalfunktion und dessen Frequenzspektrum hat diese Spiegelung keinen negativen Einfluss.

Abbildung: Spiegelung von nicht geraden Funktionen PC

Abbildung: Spiegelung von nicht geraden Funktionen PDA_Phone

Abbildung: Spiegelung von nicht geraden Funktionen

Die Kosinustransformation berechnet das Spektrum jener Funktion, die sich aus der Originalfunktion (rechts) und dessen Spiegelung (links) zusammensetzt.

Diskrete Fouriertransformation für Bild- und Audiokodierung

1

Eigenschaften DFT

Abbildung: Spektrum von FT/DFT PC

Abbildung: Spektrum von FT/DFT PDA_Phone

Abbildung: Spektrum von FT/DFT

• nichtperiodische kontinuierliche Funktion - kontinuierliches Spektrum
• diskrete Funktion
  • diskretes Spektrum
  • Anzahl der Werte im Originalbereich = Anzahl der Werte im transformierten Bereich

Nachteile der DFT bei der Bild- und Audiokodierung

• Original- und Frequenzbereich stark von einander getrennt
  • Originalbereich - keine stationäre Frequenzinformation
  • Frequenzbereich - keine Information wann (bzw wo) eine bestimmte Frequenz
• Manipuation der DFT Koeffizienten
  • Änderung eines Wertes im Originalbereich - Änderung aller Werte im Frequenzbereich
  • Änderung eines Wertes im Frequenzbereich - Änderung aller Werte im Originalbereich

Applet: Fouriertransformation applet40301 source und jar vorhanden

Also available at http://www.ims.tuwien.ac.at/%7Emigl/modul4-appletsammlung/40301/index.html

2

Die Signalfunktionen von digitalen Bildern und digitalem Audio sind keine kontinuierlichen Funktionen, sondern diskrete. Für diese Art von Signalen wurde die Diskrete Fouriertransformation (DFT) entwickelt.

Eigenschaften DFT

• Ist das Signal im Zeit- bzw im Ortsbereich diskret, so hat es auch ein diskretes Frequenzspektrum
• Anzahl der diskreten Werte im Zeitbereich (bzw im Ortsbereich) ist gleich Anzahl der Werte im Frequenzspektrum
• Mit Hilfe der iDFT 495 gelangt man vom Frequenz- zurück in den Originalbereich (Ort oder Zeit)

Abbildung: Spektrum von FT/DFT PC

Abbildung: Spektrum von FT/DFT PDA_Phone

Abbildung: Spektrum von FT/DFT

a. FT eines instationären, kontinuierlichen Signals b. DFT eines diskreten Signals

Spektren füe multmediale Daten

Für die Bildkodierung entspricht die x-Achse den Pixeln einer Bildzeile, die Funktionswerte sind Helligkeitswerte (bzw. Farbwerte) der jeweiligen Pixel. Für die Audiokodierung ist die x-Achse die Zeitachse, die Funktionswerte sind die Amplitudenwerte. Im Frequenzbereich ist die x-Achse die Frequenz, die Funktionswerte sind die Amplitudenwerte der entsprechenden harmonischen Schwingungen. Für Audiosignale sind die Frequenzen die im Signal vorkommenden Töne, die Funktionswerte deren Intensitäten.

Nachteile der DFT bei der Bild- und Audiokodierung

Die im folgenden beschriebenen Nachteile der Fouriertransformation können mit Hilfe des Applets 40301 leicht verifiziert werden.

Trennung Original/Frequenzbereich

Bei der DFT gibt es zwei streng von einander getrennte Bereiche.

• Im Originalbereich werden ausschließlich Signalwerte als Funktion der Zeit oder als Funktion des Ortes dargestellt, es gibt keinerlei Hinweise auf Frequenzeigenschaften bestimmter Stellen des Signals. Für ein Musiksignal zum Beispiel bedeutet das, man hat keine Möglichkeit im Originalbereich herauszufinden, welche Töne zu einem bestimmten Zeitpunkt gespielt werden.
• Im Frequenzbereich werden alle im Signal vorkommenden Frequenzkomponenten dargestellt, aber es gibt keinerlei Informationen, welche Frequenzkomponenten für welchen Zeitpunkt (bzw Ort) des Signals signifikant sind. Für ein Bild kann man aus dem Frequenzspektrum zwar herauslesen, ob starke Kanten vorhanden sind, aber man weiß nicht, wo sie sich im Originalbereich befinden. Für Audiodateien kennt man alle im Signal vorkommenden Töne in Bezug auf Tonhöhe und Lautstärke, man hat aber keinerlei Information, zu welchem Zeitpunkt welcher dieser Töne erklingt.

Manipulation der DFT-Komponenten

Komprimierungstechniken, die eine Transformationskodierung zur Datenkompression verwenden, basieren stets auf einer Manipulation der Frequenzkomponenten im Frequenzspektrum. Manipuliert man nun bestimmte DFT-Komponenten, wirkt sich diese Manipulation auf das Signal im gesamten Original aus. Es ist nicht möglich, Frequenzanteile nur für einen bestimmten Zeitpunkt (bzw für einen bestimmten Ort) zweckmäßig zu verändern.

Applet: Fouriertransformation applet40301 source und jar vorhanden

Beschreibung Applet Fouriertransformation

Das Amplituden-Zeit-Fenster links oben zeigt die blaue Linie das Signal. Die schwarzen Abtastpunkte können verschoben werden, sodass beliebige Signale gezeichnet werden können. Die Preset-Buttons darunter stellen typische Signalformen zur Verfügung, der Random-Button erzeugt ein zufälliges Signal.

Im Amplituden-Frequenz wird das Resultat der DFT 496 visualisiert. Jeder Balken steht für eine Basis-Frequenz. Links sind die tiefen Frequenzen, rechts die hohen. Der Balken ganz links steht für die vertikale Verschiebung des Signals (Offset). Auch in diesem Fenster sind Eingriffe mit der Maus möglich. Man kann das Frequenzbild des Signals verändern, d.h. gewisse Anteile des Signales betonen oder auch entfernen. Natürlich hat dies Einfluss auf das ursprüngliche Signal. Dieses wird vom Applet in Echtzeit (im Amplituden-Zeit-Fenster) aktualisiert.

Das Approximations-Fenster bietet die Möglichkeit, die Anzahl der Basis-Frequenz-Komponenten des transformierten Signals zu reduzieren. Mit Hilfe des Schiebereglers kann man die gewünschten Komponenten beliebig selektieren. Resultat ist das Approximations-Signal, welches zusammen mit dem "alten" Signal in beide Darstellungs-Fenster, in gelber Farbe, gezeichet wird. Befindet sich der Regler ganz rechts, so sind alle Komponenten des Signals selektiert und es findet keine Reduktion statt. Das Approximations-Signal und das ursprüngliche Signal sind deckungsgleich. Mit dem "Select only one frequency"-Knopf kann man genau eine gewünschte Frequenz selektieren. Diese wird zugleich in das Amplituden-Zeit Fenster gezeichnet.

Instruktionen

• Das Preset "Sinus" besitzt nur den niedersten Freuqenzanteil, "glatte" Signale (zB Triangel) besitzen kaum hochfrequente Komponenten.
  • Zeichne in beiden Fenstern ein glattes Signal mit wenigen hohen Frequenzen! Wie sieht ein Signal mit hohen Frequenzanteilen aus? Gib in beiden Fenstern ein solches Signal ein! Tipp: Man kann das Signal mit dem Preset "Flat" zurücksetzen.
• Verändere den Offset (1. Balken im Amplituden-Frequenz-Fenster).
  • Wieso verschiebt sich die Frequenz in vertikaler Richtung? Wie und warum ändert sich der Klang und Lautstärke des Signals?
• Benutze den Schieberegler "Approximation Quality" bei den verschiedenen Presets. Wie entwickelt sich die Annäherung?
• Gib ein Signal ein, dass alle Frequenzanteile beinhaltet. Aktiviere das Häckchen "Select only one frequency" und gehe mit dem Schieberegler die einzelnen Frequenzen durch (gelbe Linie). In welchen Verhältnis stehen sie? Wie agieren sie miteinander?

Also available at http://www.ims.tuwien.ac.at/%7Emigl/modul4-appletsammlung/40301/index.html

3

Link auf zum Thema passendes Applet

Fast Fouriertransformation Applet40305 nur als hyperlink

Kurzbeschreibung

Ein Applet zur Veranschaulichung der Fast Fourier Transformation. Voreingestellte Signale werden mit den üblichen Fensterfunktionen dargestellt. Zur erwähnen wäre der optionale Anti-Aliasing Filter und das einstellbare Störsignal.

Aus den Koordinaten des Mousezeigers werden Zeit und Spannung des Signals berechnet.

Autor(en)

-

www

http://www.dsptutor.freeuk.com/analyser/SpectrumAnalyser.html

Diskrete Kurzzeit Fouriertransformation poul1999

1

Funktionsweise der Diskreten Kurzzeit Fouriertransformation

• Originalfunktion in kleine Abschnitte unterteilt
  • Bildkodierung - in 8x8 Pixel Blöcke
  • Audiokodierung - Zeitabschnitte (typisch 4ms bis 20 ms)
• Jeder Abschnitt unabhängig von den anderen transformiert

Nachteil der Diskreten Kurzzeit Fouriertransformation

Dekorrelation der Signalabschnitte

Fensterbreite unabhängig von Frequenz

• Fensterlänge ist fixiert
  • verursacht Blockartefakte
  • ist immer ein Kompromiss zwischen möglichst langem und möglichst kurzem Fenster
• Wünschenswert wäre variable Fensterlänge
  • Hohe Frequenzen
    • benötigen möglichst kurzes Fenster, dadurch genaue Zuordung im Originalbereich
  • Tiefe Frequenzen
    • möglichst lange Fenster, dadurch ein großer Bereich mit nur wenigen Koeffizienten darstellbar
    • kurze Fenster erzeugten unnötigen Datenoverhead

2

Funktionsweise der Diskreten Kurzzeit Fouriertransformation

Abhilfe gegen das Frequenz/Zeit(Ort)-Dilemma schafft die Diskrete Kurzzeit Fouriertransformation (englisch: Discrete.Short-Time Transform DSTFT 497). Es wird dazu das Signal im Originalbereich in kleine Abschnitte unterteilt. Für jeden Abschnitt wird eine eigene DFT berechnet. Frequenzkomponenten beziehen sich jetzt ausschließlich auf den betreffenden Signalabschnitt. Auch Manipulationen im Frequenzbereich wirken sich nun nur mehr auf diesen Signalabschnitt aus.

• Für Bildkodierung – Es wird das Bild in 8x8 Pixel Blöcke unterteilt. Für jeden Block wird eine Diskrete Fouriertransfomation (für JPEG ist dies eine DCT 242 ) durchgeführt. Man erhält für unterschiedliche Bildbereiche unterschiedliche Frequenzkomponenten.
• Für Audiokodierung – Das Audiosignal wird in Zeitabschnitte (4ms bis 20ms) unterteilt. Jeder Zeitabschnitt wird so durch seine für diesen Zeitpunkt signifikanten Frequenzkomponenten (mit Hilfe einer FFT 417, MDCT 493) dargestellt. Manipulationen einer Frequenzkomponente wirken sich ausschließlich auf das Signal im entsprechenden Zeitabschnitt aus.

Die Diskrete Kurzzeit Fouriertransformation ist heute die am meist eingesetzte Transformationskodierung (JPEG, MPEG-1 und MPEG-2 (Video und Audio), AC-3, teilweise in MPEG-4).

Nachteil der Diskreten Kurzzeit Fouriertransformation

Dekorrelation der Signalabschnitte

Bei der Diskreten Kurzzeit Fouriertransformation werden die verschiedenen Signalabschnitte absolut getrennt von einander analysiert. Das führt dazu, dass besonders bei sehr hoher Kompression Signaländerungen im Originalbereich, verursacht durch Manipulationen im Frequenzbereich, an den Übergängen zu den benachbarten Abschnitten störende Artefakte erzeugen.

Artefakte bei Bildkodierung

Bei der Bildkodierung werden die Frequenzkomponenten eines Blockes so manipuliert, dass auch bei hoher Kompression die auftretenden Fehler möglichst wenig störend ins Auge stechen. Mit höher werdender Kompression werden Frequenzkomponenten höherer Ordnung immer ungenauer kodiert, in Folge lässt die Bildschärfe nach, was für unser Auge akzeptierbar ist. Was für unser Auge aber störend ist, ist die Bildung eines Schachmusters über das gesamte Bild. Dieses entsteht dadurch, dass auf Grund der voneinander getrennten Transformation die Frequenzkomponenten unterschiedlicher Blöcke nicht mehr miteinander korrelieren. Durch die von einander unabhängigen Manipulationen der Komponenten entstehen an den Blockgrenzübergängen Unstetigkeitsstellen des Bildsignals (steile Signalsprünge). So werden die Grenzen der Blöcke sichtbar.

Blockbildung: Es werden die 8x8 Blöcke getrennt voneinander analysiert. Bei hoher Kompression werden die Ränder dieser Blöcke störend sichtbar.

Bei der ST Fouriertransformation ist für alle Frequenzen die Fensterbreite gleich. Für eine optimale Signalanalyse wäre aber eine frequenzabhängige Fensterbreite wünschenswert. Die Wahl der Fensterbreite der ST Transformation ist daher immer ein Kompromiss zwischen

• möglichst kurzes Fenster, um Kanten, Ecken, Umrisse etc möglichst genau darstellen zu können
• Möglichst lange Fenster, um schachbrettartige Artefakte zu vermeiden

Kurzes Fenster

Bei starken Signaländerungen innerhalb eines Signalabschnittes (steiler Anstieg des Signals) dominieren kurzfristig die sehr hohen Frequenzkomponenten. Um diese Komponenten der entsprechenden Position im Originalbereich möglichst genau zuordnen zu können, muss das Fenster möglichst kurz sein.

Langes Fenster

Bei sich weniger rasch ändernden Signalbereichen, wie ein blauer Himmel als Hintergrund, ein weiche Hautpartie in einem Portrait, ein statischer Ton eines Musikinstrumentes etc, wäre eine Fensterbreite wünschenswert, die diesem zusammenhängenden Signalbereich ein einheitliches Frequenzspektrum zuordnet. Aufgrund der geringen Frequenz benötigte man auch nicht die hohe Auflösung des Signals im Originalbereich. So könnte man mit einer geringeren Anzahl von Frequenzkoeffizienten ein langes Fenster repräsentieren. Außerdem können im Frequenzbereich Manipulationen der Frequenzkomponenten durchgeführt werden, ohne dass im Originalbereich die schachbrettartigen Artefakte entstehen.

Zusammenfassung

1

• Fouriertransformation abgeleitet von der Fourierreihe
  • Originalsignal in Frequenzbereich transformiert
  • Frequenzbereich
  • Intensität der Frequenzkomponenten
  • Phasenlage der Frequenzkomponenten
• Komplexe Zahlen
  • bestehen aus zweiTeilen (imaginär und reel), daher hervorranges Tool für Fouriertransformation
• Kosinustransformation
  • für Funktionen mit endlichem Startpunkt Imaginärteil gleich Null
  • dadurch nur halbierter Rechenaufwand
• Short time FT
  • Signale in Abschnitte unterteilt
  • Vorteil
    • Zusammenhang zwischen Original- und Frequenzbereich
  • Nachteil
    • Dekorrelation der Abschnitte

2

Fourierreihe

Ursprünglich als Fourierreihe konzipiert, ist die Fouriertransformation heute eines der wichtigsten Tools der Signalanalyse. Auf ihr basieren auch viele andere gebräuchliche Signalanalysealgorithmen, wie zum Beispiel die Wavlettransformation. Bei der Fouriertransformation wird ein Signal (orts- oder zeitabhängig) in den so genannten Frequenzbereich transformiert. Dieser wird mit klomplexen Zahlen beschrieben, die jeweils aus zweiTeilen bestehen und Intensität und Phasenlage einer bestimmten Frequenzkomponente im Signal beschreiben. Ein Spezialfall stellen gerade Funktionen dar: Hier wird der Imaginärteil aller komplexen Koeffizienten Null. Es ist für die Transformation nur mehr der halbe Rechenaufwand erforderlich. Diese Rechenersparnis wird von der Kosinustransformation ausgenutzt: Für Funktionen, die einen endlichen Startpunkt aufweisen, muss dabei ebenfalls nur der reele Teil (=Kosinusanteil) berechnet werden. Die Kosinustransformation spielt in der Komprimierung multimedialer Daten in der Form der DCT eine dominierende Rolle. Bei allen Vorteilen hat die Fouriertransformation aber auch ihre Nachteile: Original- und transformierter Bereich sind streng voneinander getrennt. Abhilfe schafft die STFT:Sie teilt das Signal in Abschnitte, jeder davon erfährt eine eigene Transformation. Ein sich dadurch ergebender Nachteil ist die Dekorrelation dieser Abschnitte.

3

Diskrete Fouriertransformation applet40304 jar vorhanden

Beschreibung

Die Anwendung besteht aus zwei Fenstern. Das Fenster "Window Functions" läßt mit gleichnamigem Menüpunkt fünf Standardfunktionen als Eingabe zu. Das obere Diagramm zeigt die Funktion als Amplitude der Samples, die DFT davon als dB pro Frequenz.

Das Hauptfenster "Discrete Fourier Transformation" bietet die Möglichkeit, per Menüpunkt "Signal" verschiedene Standardsignale einzugeben. Natürlich kann mit der Maus auch ein Signal gezeichnet werden. Der Menüpunkt "Point Size" verändert in beiden Fenstern die Maßstäbe der x-Achsen. Das Eingangssignal wird als gesampeltes Signal und in der DFT dargestellt.

In allen Diagrammen kann das Gitter in den Diagrammen ein- und ausgeschaltet werden, in dem man die Maus darauf zieht und die Taste "G" drückt. Durch Klicken in ein Diagramm wird gezoomt.

Instruktionen

• Vergleiche die DFTs der verschiedenen Sinusfrequenzen. Welche Frequenzen werden verwendet, welchen Grund hat das Auftauchen von neuen Frequenzen?
• Was bewirkt eine Veränderung der Point Size in den verschiedenen Diagrammen?
• Wie verhalten sich komplexe Signale in den Transformationen?

Also available at http://www.see.ed.ac.uk/%7Emjj/dspDemos/EE4/tutDFT.htm

Diskrete Fouriertransformation 2 applet40309

Beschreibung

Die sechs Buttons rechts oben stellen typische Signale zur Verfügung, das Eingangssignal kann mit der Maus direkt in das Periodenfenster gezeichnet werden. Mit dem Button "Calculate" kann die Transformation durchgeführt werden. Mit den "+" und "-" Buttons wird die Anzahl der Koeffizienten verändert, mit "Table" wird eine Liste der Werte ausgegeben.

Instruktionen

• Versuche ein Signal zu skizzieren, dass einen großen Grundfrequenzanteil aber wenig höhere Anteile hat. Wie sieht ein Signal aus, dass wenig Grundfrequenzen hat, aber viele hohe Anteile?
• Wie verändern sich verschiedenen Signale, wenn man die Anzahl der Koeffizienten verändert?
• Bei welchen Signalen verändert sich das Ergebnis der Transformation stark mit der Anzahl der Koeffizienten?

Weiterführendes Tutorial

http://www.stud.tu-ilmenau.de/~getsoft/_fouriertest/ger/index2.html

Link auf zum Thema passendes Java Applet

Fourier applet40303 nur als hyperlink

Kurzbeschreibung

User kann Grundfrequenz und die Anteile der Vielfachen der Frequenz per Schieberegler einstellen und sich dann per Buttondruck anzeigen lassen. Presets können ausgewählt werden, GUI funktioniert aber nicht immer.

Autor(en)

Bruno Brolis, brolis@id-net.fr

www

http://www.see.ed.ac.uk/~mjj/dspDemos/EE4/tutDFT.html