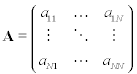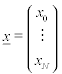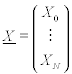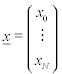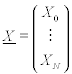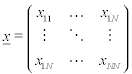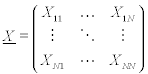Motivation effe1998, 17

1

Wozu Transformationskodierung?

• Komprimierung auf Grund perzeptueller Eigenschaften menschlicher Sinnesorgane
  • Auge empfindet Farb- und Grauwertkontraste unterrschiedlich
  • Gehör nicht allen akustischen Ereignissen gegenüber gleich empfindlich
• Was macht Transformation
  • alternative Darstellung ein und demselben Signals
  • optimale Ummünzung perzeptueller Eigenschaften in Datenreduktion

Die zwei Bereiche der Transformationskodierung

• Originalbereich für multimedialer Daten
  • Bilder - Pixelwerte
  • Audio - Amplitudenwerte als Funktion der Zeit
• Transformierter Bereich für multimedialer Daten
  • Bilder - Frequenzkoeffizienten, beschreiben analytisch Bildstrukturen
  • Audio - frequenzkoeffizienten, beschreiben Töne

2

Wozu Transformationskodierung?

Die Transformationskodierung ist ein wichtiges Werkzeug für all jene Komprimierungsalgorithmen, die zur Datenreduktion wissenschaftliche Kenntnisse über perzeptuelle Eigenschaften unserer Sinnesorgane nutzen. So weiß man, dass unser Auge gegenüber bestimmten Kontrasten besonders empfindlich ist, andere wieder werden von unserem Auge nicht so genau oder überhaupt nicht wahrgenommen (siehe Grundlagen der perzeptuellen Bildkodierung). Unser Gehör wiederum nimmt verschiedene Töne bzw Tonkombinationen unterschiedlich genau wahr (siehe Grundlagen der perzeptuellen Audiokodierung). Es sind nun oft die üblichen Darstellungen von Bild- und Audiodaten nicht besonders geeignet, diese Kenntnisse in effektive Datenreduktion ummünzen zu können. Es muss daher das Signal in einem geeigneten mathematischen Bereich dargestellt werden. Diese alternative Darstellung eines Signals (Bild oder Audio) erreicht man durch eine mathematische Transformation. Es wird dabei vom Originalbereich in den transformierten Bereich transformiert.

Definition des Transformationsbegriffes

Transformation bewirkt eine alternative Darstellung von ein und derselben Information. Eine Repräsentation einer Information geschieht im Originalbereich, die zweite im transformierten Bereich. Dabei muss gelten: Eine Änderung in einem Bereich bewirkt automatisch eine dementsprechende Änderung im anderen Bereich.

Die zwei Bereiche der Transformationskodierung

Originalbereich für multimedialer Daten

Der Originalbereich ist jener Bereich, wo multimediale Informationen entweder gesehen oder gehört werden können.

• Bilder - Originalbereich enthält die Pixelwerte eines digitalen Bildes auf einer 2-dimensionalen Ebene
• Audiosignale – Originalbereich enthält Amplitudenwerte als Funktion der Zeit

Transformierter Bereich für multimedialer Daten

Der transformierte Bereich ist für die Komprimierungsalgorithmen interessant.

• Bilder – Transformierter Bereich enthält Werte (=Koeffizienten), die die Strukturen in einem Bild beschreiben.
• Audiosignale – Transformierter Bereich enthält Werte (=Koeffizienten), die die im Signal vorkommenden Frequenzen (=Töne) beschreiben.

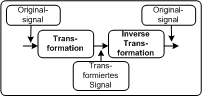
Reversibilität der Transformation

1

Transformation und ihre Inverse PC

Transformation und ihre Inverse PDA_Phone

2

Transformation und ihre Inverse PC

Im Originalbereich ist die multimediale Information durch Werte aufbereitet, mit deren Hilfe man ein Bild oder ein Tondokument direkt darstellen kann. Im transformierten Bereich hingegen kann ein Benutzer mit den Werten nicht direkt etwas anfangen. Um die Daten zu sehen oder zu hören, müssen sie zuerst wieder in den Originalbereich rücktransformiert werden. Es muss daher eine Transformation derart gestaltet sein, dass das Signal aus dem transformierten Raum wieder verlustlos in den Originalraum rück transformiert werden kann. Solche Rücktransformation bezeichnet man als Inverse Transformation.

Transformation und ihre Inverse PDA_Phone

Im Originalbereich ist die multimediale Information durch Werte aufbereitet, mit deren Hilfe man ein Bild oder ein Tondokument direkt darstellen kann. Im transformierten Bereich hingegen kann ein Benutzer mit den Werten nicht direkt etwas anfangen. Um die Daten zu sehen oder zu hören, müssen sie zuerst wieder in den Originalbereich rücktransformiert werden. Es muss daher eine Transformation derart gestaltet sein, dass das Signal aus dem transformierten Raum wieder verlustlos in den Originalraum rück transformiert werden kann. Solche Rücktransformation bezeichnet man als Inverse Transformation.

Transformationkodierung zur Datenreduktion

1

Abbildung: Transformationkodierung zur Datenreduktion PC

Abbildung: Transformationkodierung zur Datenreduktion PDA_Phone

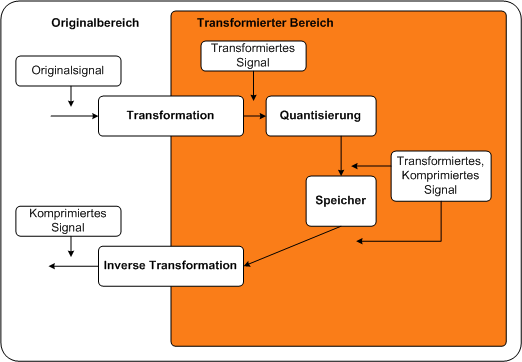
2

Abbildung: Transformationkodierung zur Datenreduktion PC

Abbildung: Transformationkodierung zur Datenreduktion PDA_Phone

Datenreduktion durch Transformationkodierung

Im Diagramm ist die prinzipielle Arbeitstechnik eines auf Transformationskodierung basierenden Algorithmus dargestellt.

1. Originalsignal wird transformiert, hier findet noch keine Datenreduktion statt.
2. Quantisierung - Quantisierung ist jener Schritt, bei der die eigentliche Kompression stattfindet. Das transformierte Signal wird unter Berücksichtigung der perzeptuellen Eigenschaften der menschlichen Sinnesorgane darauf hin untersucht, welche Informationen für die Kodierung weggelassen werden können.
3. Die quantisierten Werte des transformierten Bereiches werden gespeichert.
4. bei Abfrage werden die gespeicherten Werte in den Originalbereich rück transformiert, der Benutzer kann hier die Datei sehen oder hören. War die Quantisierung optimal, kann der Benutzer keinen qualitativen Unterschied zum Original erkennen, obwohl durch die Quantisierung Signalinformation verloren gegangen ist.

Transformationskodierung bei Bildkompression

1

Originalbereich in einem digitalern Bild

Kompression im Originalbereich PC

Originalbild
Pixelreduktion 1:10	Reduktion Bit/pixel 1:8

Kompression im Originalbereich PDA_Phone

Originalbild

Pixelreduktion, 1:10

Reduktion Bit per Pixel, 1:8

Kompression im transformierten Bereich all

JPEG ca. 1:20

Artefakte bei ca. 1:40

2

Originalbereich in einem digitalern Bild

Der Originalbereich eines digitalen Bildes ist der Ortsbereich. dort wird es durch ein zweidimensionales Gitter von Pixeln dargestellt. Jedes Pixel gibt den Grauwert beziehungsweise den Farbwert am entsprechenden Ort an. Die Größe der Bilddatei ergibt sich einerseits aus der Bitanzahl, die zur Kodierung eines Pixelwertes verwendet wird, die so genannte Pixelwortlänge, andererseits aus der Gesamtanzahl der Pixel.

Kompression im Originalbereich

Datenreduktion kann man erzielen:

• Reduktion der Pixelanzahl: das entspricht einer Reduktion der Auflösung, Bild verliert an allgemeiner Schärfe
• Reduktion der Bitanzahl/Pixel: Den Pixels werden geringere Wortlängen zugewiesen, die Farben können nicht mehr wirklichkeitsgetreu dargestellt werden
• Reine Entropiekodierung. Wird zum Beispiel bei der GIF Komprimierung angewandt (siehe Vergleich von Komprimierungsverfahren)

Bildbeispiel Komprimierung im Originalbereich PC

Originalbild
Reduktion der Pixelanzahl: Für das Bild wurde nur jedes 10 Pixel kodiert. Das entspricht einer Datenreduktion von 1:10. Die fehlenden Pixel werden bei der Reproduktion durch Ingterpolation erzeugt.	Reduktion der Bit/Pixel: Für das Originalbild werden 24 Bit pro Pixel, für oberes hingegen nur 3 Bit verwendet. Das entspricht einer Kompression 1:8

Bildbeispiel Komprimierung im Originalbereich PDA_Phone

Reduktion der Pixelanzahl: Für das Bild wurde nur jedes 10 Pixel kodiert. Das entspricht einer Datenreduktion von 1:10. Die fehlenden Pixel werden bei der Reproduktion durch Ingterpolation erzeugt.

Reduktion der Bit/Pixel: Für das Originalbild werden 24 Bit pro Pixel, für oberes hingegen nur 3 Bit verwendet. Das entspricht einer Kompression 1:8

Transformierter Bereich in einem digitalen Bild

Im transformierten Bereich wird das Bild durch so genannte Frequenzkoeffizienten dargestellt. Der DC 494 - Koeffizient beschreibt den mittleren Grau- beziehungsweise den mittleren Farbwert, Koeffizienten höherer Ordnung (-Wechselkomponenten) beschreiben Konturen, Ecken, Umrisse etc. in einem Bild.

Kompression im transformiertem Bereich

In diesem Darstellungsbereich kann man Datenreduktion erreichen, indem man Koeffizienten höherer Ordnung – diese stehen für scharfe Kanten, Umrisse etc - mit einer geringeren Genauigkeit kodiert (=Quantisierung). Auch diese Reduktion wird ab einer bestimmten Kompressionsrate sichtbar (weniger detailgetreue Darstellung des Bildes, vor allem eine Verminderung der Bildschärfe an scharfen Kanten), aber diese Artefakte sind im Vergleich zu jenen, hätte man im Originalbereich komprimiert, bedeutend weniger störend und treten erst bei einer höheren Kompressionsrate auf. Viele Bildkodierungstechniken, wie JPEG, JPEG2000 etc. arbeiten im transformierten Bereich.

Kompression im Frequenzbereich all

JPEG ca. 1:20: Zwischen Original und komprimierten bild ist so gut wie kein Unterschied zu erkennen.

JPEG ca. 1:40: bei höheren Kompressionsfaktorenen werden bei JPEG schachbrettartige Artefakte sichtbar.

Transformationskodierung bei Audiokompression

1

Originalbereich

Kompression im Originalbereich

• Reduktion Abtastfrequenz
• Reduktion Bit/Abtastwert
• Entropy, Prädiktionskodierung

Hörbeispiel

Kompression im transformierten Bereich

• Berücksichtigung spektraler Eigenschaften unseres Gehörs
  • Töne ,die wir gut wahrnehmen, werden genau kodiert
  • Töne, die wir schlecht wahrnehmen, werden nur mit wenig Bit kodiert

Hörbeispiel

2

Originalbereich eines digitalen Audiosignals

Der Originalbereich eines digitalen Audiosignals ist der Zeitbereich (siehe Modul1,“4.3 Digitalisierung von Audiosignalen“ ???? ). Es werden die in einem fixen Zeitabstand abgetasteten Amplitudenwerte angegeben. Die Größe der Datei ergibt sich aus der Bitzahl, die zur Kodierung eines Amplitudenwertes verwendet wird, andererseits aus der Anzahl der Amplitudenwerte pro Zeiteinheit.

Kompression im Originalbereich

Datenreduktion kann man erzielen:

• Reduktion Abtastfrequenz - Eine Reduktion der Abtastfrequenz reduziert die Bandbreite des Audiosignals. Bei geringer Bandbreite erhält man einen Telefoneffekt
• Reduktion der Bitanzahl/Amplitudenwert - die Amplitudenwerte werden in einer gröberen Auflösung gespeichert. Bei der Wiedergabe macht sich diese Ungenauigkeit durch Quantisierungsrauschen (siehe Grundlagen der perzeptuellen Audiokodierung) störend bemerkbar. Die Aufnahmen klingen stark verrauscht.
• Reine Entropiekodierung, Prädiktionskodierung - Wird zum Beispiel von MPEG-2 Audio/AAC im verlustlosen Modus verwendet

Hörbeispiel zur Datenreduktion im Originalbereich

Tranformierter Bereich eines digitalen Audiosignals

In diesem Darstellungsbereich werden nicht mehr die Amplitudenwerte als Funktion der Zeit betrachtet. Vielmehr werden durch eine Transformation alle im Signal vorkommenden Töne (=Frequenzen) und deren Intensitäten angegeben.

Kompression im transformierten Bereich

Unser Hörempfinden besitzt aus physio- und psychologischen Gründen starke spektrale Eigenschaften (siehe Grundlagen der perzeptuellen Audiokodierung). Wir können bestimmte Töne besser, andere wieder weniger gut hören. Auch das gleichzeitige Auftreten verschiedener Tönen wird von unserem Gehör unterschiedlich genau wahrgenommen. So kann in diesem transformierten Bereich viel an Information durch grobe Quantisierung entfernt werden, ohne dass unser Ohr diesen Informationsverlust hört. Viele Kodierungstechniken, wie MP3, AAC, AC-3 etc., arbeiten im transformiertem Bereich.

Hörbeispiel zur Datenreduktion im transformierten Bereich

Für das folgende Beispiel wurde eine Audiodatei im Original- , die andere im transformiertem Bereich komprimiert. In beiden Fällen wurde eineKompression von 1:14 erzielt.

Diskrete Transformationen stru2002, ab 86

1

allgemeine diskrete Transformation

• Transformationskern
• inverse Transformation

Mathematische Darstellung der Diskreten Transformation

... diskrete Transformation

... inverse Transformation

Matrixschreibweise

mit

2

auto

Bei digitalen multimedialen Daten (Audio oder Bildsignale) handelt es sich ausschließlich um diskrete Signale. Das heißt, die Anzahl der im Originalbereich enthaltenen Werte ist eine endlich große, ganzzahlige Zahl. Für Bilddateien sind das Bildpunkte (pixel), für Audiodateien sind es Amplitudenwerte.

allgemeine diskreteTransformation

Jede diskrete Transformation enthält einen Transformationskern. Durch diesen Kern werden die Werte des Originalbereiches mit den Werten des transformierten Bereiches in einen mathematisch eindeutigen Zusammenhang gebracht. Um eine eindeutige Rücktransformation zu gewährleisten, muss weiters gelten:

Anzahl der Werte im Originalbereich = Anzahl der Werte im tranformierten Bereich

Mathematische Darstellung der Diskreten Transformation

mit

.......	Werte im Originalbereich
.....	Werte im transformierten Bereich
............	Anzahl der Werte
..	Transformationskern

Mathematische Darstellung der inversen diskreten Transformation

mit

...Kern der Rücktransformation

Matrixschreibweise diskrete Transformation

mit

	Transformationskern
	Werte im Originalbereich
	Werte im transformierten Bereich

Matrixschreibweise inverse Transformation

mit

Ein- und zweidimensionale Transformationen

1

Eindimensionale Transformation: Audiosignal

Zeitbereich - einzige Variable: Amplitudenwert als Funktion der Zeit PC

Zeitbereich - einzige Variable: Amplitudenwert als Funktion der Zeit PDA_Phone

Transformierter Bereich - einzige Variable: Frequenzkoeffizient als Funktion der Frequenz PC

Transformierter Bereich - einzige Variable: Frequenzkoeffizient als Funktion der Frequenz PDA_Phone

Zweidimensionale Transformation: Digitales Bild

• Ortsbereich - zwei Variablen: Pixelwert als Funktion der x- und y-Achse
• Transformierter Bereich - zwei Variable: Koeffizienten als Funktion von vertikaler und horizontaler Frequenz

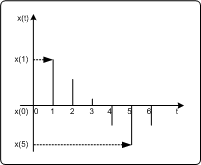
2

Eindimensionale Transformationen

Mit der oben angegebenen Gleichung können diskrete Funktionen mit einer Variablen transformiert werden.

Eindimensionale Transformation: Audiosignal

Zeitbereich

Amplituden Werte mit der Variable Zeit

Abbildung: Zeitbereich - einzige Variable: Amplitudenwert als Funktion der Zeit PC

Abbildung: Zeitbereich - einzige Variable: Amplitudenwert als Funktion der Zeit PDA_Phone

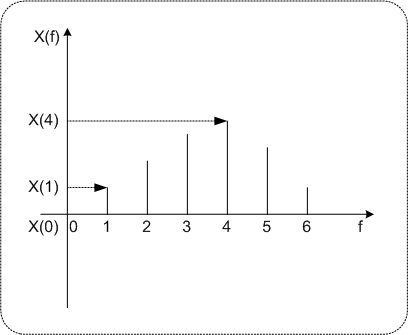
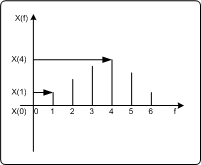
Transformierter Bereich

Amplitudenwerte mit der Variablen Frequenz

Abbildung: Transformierter Bereich - einzige Variable: Frequenzkoeffizient als Funktion der Frequenz PC

Abbildung: Transformierter Bereich - einzige Variable: Frequenzkoeffizient als Funktion der Frequenz PDA_Phone

Zweidimensionale Transformation

Digitale Bilder werden im Originalbereich durch ihre Pixelwerte dargestellt. Die Position jedes Pixels wird durch seine x-und y-Achse Komponenten .angegeben. Die Pixelwerte sind also von 2 Variablen abhängig.

Zweidimensionale Transformation: Digitales Bild

Originalbereich

Jedem Pixel ist ein bestimmter Wert zugeordnet

... ist der Helligkeitswert (oder Farbwert) des Pixels an der Position x,y.

Transformierter Bereich

...Wert mit den Frequenzwerten u,v.

Transformationen für die Praxis

1

Unterschiedliche Transformationen

• Einziger Unterschied - Transformationskern

Für Multimediale Dateien häufig verwendete Transformationen

• Bild
  • DCT 242 - JPEG 29
  • Wavelet - JPEG2000
• Audio
  • MDCT 493 - zur Unterteilung des Signals in Subbands
  • FFT 417- Signalanalyse für psychoakustisches Modell

2

Unterschiedliche Transformationen

Es wurden für die verschiedenen Anwendungen verschiedene Transformationen entwickelt. Sie leiten sich alle von der allgemeinen Darstellung der diskreten Transformation (und dessen Inversen) ab . Verschiedene Transformationen unterscheiden sich ausschließlich im Transformationskern.

Für Multimediale Dateien häufig verwendete Transformationen

Die Mutter aller Transformationen ist die Fouriertransformation. Die Mehrzahl der zur Audio - und Bildkomprimierung verwendeten Transformationen leiten sich von ihr ab. Die Fouriertransformation stellt immer das Frequenzspektrum einer Funktion dar.

Bild

DCT

Für die Bildkompression kommt im JPEG 29 Standard die DCT 242 (Der JPEG Standard und JPEG Bildvorbereitung) zum Einsatz. Sie ist eine auf Einfachheit optimierte Version der Fouriertransformation und ist besonders zur Approximation von Signalen mit relativ glattem Verlauf geeignet. Das macht sie ideal für die Bildkomprimierung. Durch die geringe Komplexität der Algorithmen ist gewährleistet, dass JPEG auch bei einfach aufgebauter Hardware (z.B. einfache digitale Fotokamera) implementiert werden kann.

Wavelet Transformation

Die Wavelettransformation wird im JPEG2000 Standard verwendet. Sie bringt gegenüber der DCT 242 eine deutlich bessere Bildqualität (siehe JPEG versus JPEG2000), stellt aber bezüglich Komplexität höhere Ansprüche.

Audio

Für die Audiokompression werden vorwiegend die Fast Fouriertransformation, und die MDCT 493 verwendet. (Siehe Fouriertransformation)

Modifizierte DCT pere2002

Die Modifizierte Diskrete Kosinustransformation spielt eine elementare Rolle bei Audioencodern wie mp3 und AAC. Es werden dabei nicht nur die Werte des soeben bearbeiteten Signalabschnittes (=Fenster) in die Frequenzanalyse mit einbezogen, sondern auch Werte der beiden unmittelbar benachbarten Signalabschnitte. Die MDCT arbeitet dabei mit einer 50 prozentigen Überlappung der Fenster.

Vorteil MDCT für Audiokodierung

Es entsteht keine Blockartefakte. Bei Verwendung einer gewöhnlichen DCT würde bei höheren Kompressionen die Blockartefakte als störenderTon hörbar werden.

Fast Fouriertransformation

Zur psychoakustischen Beurteilung (siehe Grundlagen der perzeptuellen Audiokodierung) des Frequenzbereiches eines Audisignals sind auch die Phaseninformationen der einzelnen Frequenzkomponenten wichtig. Diese werden bei der DCT allerdings nicht berücksichtigt. Daher kommt hier die FFT 417 zum Einsatz. Sie ist eine auf schnelle Rechenzeit optimierte Version der Fouriertransformation.

Weitere Transformationen

1

Karhunen-Loeve Transformation (KLT)

• Vorteil - optimale Dekorrelation der Signalwerte
• Nachteil - es gibt keinen fixen Transformationskern, Kern uss immer in kodierung mit einbezogen werden

Walsh Hadamard Transformation (WHT)

• optimiert für starke Signalanstiege
• bei Bild- und Audiosignalen meist runder Verlauf, WHT wird hier nicht eingesetzt

2

Karhunen-Loeve Transformation KLT stru2002

Die KLT wird auch als Hauptachsen Transformation bezeichnet

• Vorteil: Sie realisiert eine optimale Dekorrelation der Signalwerte. Es ist kein bestimmter Transformationskern definiert, sondern dieser hängt vom Signal selbst ab.stru2002,89
• Nachteil: Die Transformation ist sehr rechenintensiv. Für die Datenreduktion ist weiters nachteilig, dass neben den eigentlichen Daten immer der verwendete Transformationskern mitkodiert werden muss.

Walsh Hadamard WHT stru2002

Die WHT ist im Vergleich zur DCT 242 zur Approximation von Signalen mit starken Signalanstiegen im Originalbereich optimiert. Starke Signalanstiege entsprechen in Bildern abrupte Grauwertänderungen (ein Pixel ist weiß, dass unmittelbar danebenliegende schwarz). In natürlichen Bildern sind solche Sprünge sehr selten. Das ist der Grund, dass die Entwickler von Bildkomprimierungsalgorithmen meist die DCT 242 der Walsh Hadamard Transformation vorziehen.