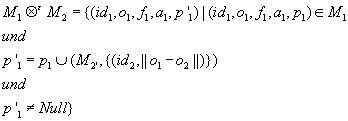Codeformatierung sieh LU10+11.ppt - Done, please check and remove xIgnore. Done (bt).

Urheberrechthinweis in LOD2 ausgebessert.

"siehe Folie" geändert.

Acronyme, Absätze, Wordanführungszeichen done.

Review von Prof. Kosch eingearbeitet.

Formeln inline gestellt.

Beispiele von Multimedia Anfragen

1

Multimedia Anfragen - Beispiel

Auto PC

Auto PDA_Phone

Auto

Zwei Bildtabellen ÜB und MA:

• ÜB(Foto, SigVektor, Zeit, Datum) -- Überwachungsbilder
• MA(Foto, SigVektor, Name, Tätigkeit) -- Mitarbeiter

Anfrage 1: Finde ausgehend von einem bestimmten Bild einer Person in Tabelle ÜB die ähnlichsten Fotos in der Tabelle MA.

• Diese Anfrage ist üblich in bestehenden Systemen.
• Für weitere Details von Anfragen siehe LU Überblick über Management- und Abfragesprachen und LU Multimedia Object Query Language.

Betrachten wir ein weiteres Beispiel:

Anfrage 2: Für alle Bilder in Tabelle ÜB, die gestern zwischen 16:00 und 18:00 aufgenommen wurden, sollen die ähnlichsten Bilder in Tabelle MA ausgegeben werden, samt ihrer zugehörigen Namen und Adressen.

• Diese Anfrage wird von bestehenden Systemen nicht unterstütz
• Benötigt eine relationale Selektion auf der Tabelle ÜB und einen "ähnlichkeitsbasierten Join" über die Tabellen ÜB und MA

Betrachten wir Anfrage 2:

• ÜB(id, ÜB_Foto, SigVektor, A', P), wobei A' eine Objektkomponente ist:
  • A' = {Datum, Zeit}. ÜB_Foto ist das Foto, das von der Überwachungskamera aufgenommen wurde.
• MA(id, Foto, SigVektor, A*, P), wobei die Komponente A* aus dem Schema
  • A*(MAName, MAAdresse, Abteilung, Tätigkeit) besteht und Foto das Foto des Mitarbeiters ist.
  
  

Die Anfrage lautet in einer Anfragesprache wie SQL:

Anfrage

SELECT *
FROM ÜB, MA
WHERE ÜB.F ≈ MA.F
	AND ÜB.A'.Datum = 31-12-2003
	AND ÜB.A'.Zeit BETWEEN (16:00 AND 18:00);

Auto

• Das Symbol "≈"steht für die ähnlichkeitsbasierte Join-Operation (siehe später).

2

Multimedia Anfragen - Beispiel

Anfragen auf Multimediadatenbanksysteme werden mit der steigenden Masse an gespeicherten Multimediadaten immer häufiger eingesetzt, wie das Anwendungsbeispiel einer Überwachungskamera zeigt.

Auto PC

Auto PDA_Phone

Auto

Obige Abbildung veranschaulichen ein computergestütztes Überwachungssystem in einem Bürogebäude. Eine Überwachungskamera im Eingangsbereich nimmt von jeder Person, die das Gebäude betritt, ein Bild auf. Dieses Bild wird in die Datenbanktabelle ÜB gespeichert. Ein Eintrag in dieser Tabelle beinhaltet neben dem Überwachungsbild auch einen Signaturvektor (z.B. Farbhistogramm) des jeweiligen Bildes. Zeit und Datum der Aufnahme werden ebenfalls gespeichert. Eine zweite Tabelle MA beinhaltet Informationen über die Mitarbeiter im Bürogebäude. Neben textuellen Informationen wie Name und Tätigkeit wird in dieser Tabelle auch ein Foto des Mitarbeiters samt Signaturvektor gespeichert. Das relationale Schema der zwei Tabellen lässt sich wie folgt darstellen:

ÜB(Foto, SigVektor, Zeit, Datum)
MA(Foto, SigVektor, Name, Tätigkeit)

Eine sinnvolle Anfrage auf diesem Schema wäre zum Beispiel:
Finde ausgehend von einem bestimmten Bild einer Person in Tabelle ÜB die ähnlichsten Fotos in der Tabelle MA.

Diese und ähnliche Anfragen basierend auf Metadaten werden von bestehenden Datenbanksystemen weitgehend unterstützt.
Weitere Details über Anfragen in Multimedia-Datenbanken findet man in LU Überblick über Management- und Abfragesprachen und LU Multimedia Object Query Language

Betrachten wir ein weiteres Beispiel:

Für alle Bilder in Tabelle ÜB, die gestern zwischen 16:00 und 18:00 aufgenommen wurden, sollen die ähnlichsten Bilder in Tabelle MA ausgegeben werden, samt ihrer zugehörigen Namen und Adressen.

Diese Anfrage wird von bestehenden Datenbanksystemen nicht unterstützt. Hier wäre es nötig, mehrere Operationen in den Tabellen durchzuführen, da umfassende Informationen der Personen gefragt sind, deren Bilder in der Tabelle ÜB gespeichert sind. Durch ähnlichkeitsbasierte Operationen werden keine präzisen Vergleiche durchgeführt, deshalb ist es üblich nach einer Reihe sehr ähnlicher Bilder zu suchen.

Um die obige Anfrage durchzuführen, benötigt man eine relationale Selektion auf der Tabelle ÜB und einen ähnlichkeitsbasierten Join über die Tabellen ÜB und MA. Es müssen also relationale und ähnlichkeitsbasierte Operationen in Bildtabellen kombiniert und verarbeitet werden.

Noch einmal zur Anfrage 2, die vorher behandelt wurde:
Für alle Bilder in Tabelle ÜB, die gestern zwischen 16:00 und 18:00 aufgenommen wurden, sollen die ähnlichsten Bilder in Tabelle MA ausgegeben werden, samt ihrer zugehörigen Namen und Adressen.

Gegeben sei das folgende relationale Schema:
ÜB(id, ÜB_Foto, SigVektor, A', P), wobei A' eine Objektkomponente ist: A' = {Datum, Zeit}. ÜB_Foto ist das Foto, das von der Überwachungskamera aufgenommen wurde.
MA(id, Foto, SigVektor, A*, P), wobei die Komponente A* aus dem Schema A*(MAName, MAAdresse, Abteilung, Tätigkeit) besteht und Foto das Foto des Mitarbeiters ist.

In einer Anfragesprache wie SQL könnte man somit die obige Anfrage wie folgt formulieren:

Anfrage

SELECT *
FROM ÜB, MA
WHERE ÜB.F ≈ MA.F
	AND ÜB.A'.Datum = 31-12-2003
	AND ÜB.A'.Zeit BETWEEN (16:00 AND 18:00);

Auto

Das Symbol "≈" steht hierbei für die ähnlichkeitsbasierte Join-Operation. Diese Operationen werden später detaillierter behandelt.

Anforderungen der Multimedia Anfrageverarbeitung und Optimierung

1

Auto

Multimedia Anfrageverarbeitung und -optimierung beinhaltet:

• Definition des Datenmodells für die Behandlung von multimedialen Daten
• Definition von multimedialen Operationen wie z.B. "Ähnlichkeitsbasierte Selektionen und Joins",
• Entwicklung einer formalen Algebra für Anfrageoperationen in Multimediadatenbanken
• Entwicklung von Strategien für die Optimierung von multimedialen Anfragen (siehe LU Multimedia Anfrageoptimierung)

Allgemeine Ziele

DBMS401:

• Metadaten zum Beschreiben/Suchen von Bildern (üblich seit ca. 20 Jahren)
• relationaler Vergleich von Schlüsselwörtern
  aber,
  • unvollständige Darstellung von Bildern,
  • subjektive Beschreibungen,
  • zeitraubend.

Computer Vision:

• versprechende CBIR423-Methoden (üblich seit ca. 10 Jahren)
• Automatische Extrahierung des Inhalts,
• Beschreibung: durch Farbe, Textur, Form
• aber,
  • ähnlichkeitsbasiert (kein genauer Vergleich)

Ein System mit Anfragen auf Bilder und mehreren Kriterien:

• verwendet ein OR Modell,
• praktisches Repository Modell der Bilddaten,
• basierend auf einer neuen ähnlichkeitsbasierten Algebra,
• Anfrageoptimierung ist möglich.
  

2

Auto

Die Anfrageverarbeitung und -optimierung in multimedialen Datenbanken beinhaltet speziell folgende Punkte:

• Die Definition eines Datenmodells für multimediale Daten, um die Speicherung und die Anfragen mit mehreren Kriterien zu erleichtern.
• Das Definieren von multimedialen Operationen wie zum Beispiel "ähnlichkeitsbasierte Selektionen und Joins", damit umfassende Anfragen auf Bildtabellen durchgeführt werden können.
• Die Entwicklung einer formalen Algebra für Anfrageoperationen in Multimediadatenbanken, welche die Modellierung, Optimierung und Verarbeitung von multimedialen Anfragen unterstützt und außerdem ähnlichkeitsbasierte und relationale Operatoren kombiniert.
• Die Entwicklung von Strategien für die Optimierung von multimedialen Anfragen. Dieser Punkt wird in LU Multimedia Anfrageoptimierung näher behandelt.

Allgemeine Ziele

Die Möglichkeiten der Anfrageverarbeitung und Optimierung, die in herkömmlichen Datenbanksystemen zur Verfügung gestellt werden, können den Anforderungen in multimedialen Datenbanken oft nicht genügen.

Im Folgenden werden die Möglichkeiten verschiedener Ansätze einer Anfrageverarbeitung betrachtet.
In relationalen Datenbankmanagementsystemen gibt es schon seit ungefähr 20 Jahren die Möglichkeit, Metadaten zum Beschreiben bzw. Suchen von Bildern zu verwenden. Die Anfrageverarbeitung erfolgt durch einen relationalen Vergleich von Schlüsselwörtern. Bilder können jedoch nur unvollständig dargestellt werden, außerdem sind Metadaten auf subjektive Beschreibungen beschränkt, die zeitraubende Eingaben erfordern.
Auf der anderen Seite gibt es schon seit etwa 10 Jahren versprechende CBIR423-Methoden (content-based information retrieval), die eine automatische Extrahierung des Inhalts ermöglichen. Außerdem können multimediale Inhalte durch Farbe, Textur oder Form beschrieben werden. Bei diesem Ansatz besteht jedoch das Problem, dass Anfragen nur ähnlichkeitsbasiert durchgeführt werden können, das heißt ein genauer Vergleich ist nicht möglich.
Ein System mit Anfragen auf Bilder und mehreren Kriterien setzt Ansätze von beiden Seiten voraus. Gefordert wird die Verwendung eines objektrelationalen Modells und eines praktischen Repository Modells der Bilddaten. Die Anfrageverarbeitung basiert auf einer neuen ähnlichkeitsbasierten Algebra, wobei eine Anfrageoptimierung möglich ist.

Modellierung von Bilddaten

1

Auto

Auto PC

Auto PDA_Phone

2

Auto

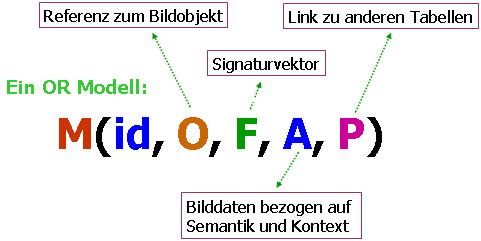
Um eine Anfrageverarbeitung und Optimierung für multimediale Daten zu erleichtern, muss eine geeignete Darstellung der Bilddaten gefunden werden. Einen objektorientierten Ansatz bietet das Repository Modell der Bilddaten. Dieses Modell kann als Bildtabelle mit fünf Komponenten betrachtet werden:

M(id, O, F, A, P)

• Die Komponente 'id' dient als eine eindeutige Bezeichnung für eine Instanz aus M.
• O ist eine Referenz zum Bildobjekt selbst, das entweder als BLOB407 in der Tabelle gespeichert, oder als externes BFILE referenziert werden kann.
• F ist der Signaturvektor, der eine Repräsentation des referenzierten Bildes O darstellt.
• A stellt eine Attributkomponente dar, die zur Beschreibung des Bildobjekts verwendet wird. Verwendet werden Schlüsselwörter, die Semantik, Kontext und räumliche Bilddaten annotieren. Diese Komponente kann auch als eine Menge von Objekttypen deklariert sein.
• Die letzte Komponente P ist eine Datenstruktur, die Links zu Instanzen anderer Tabellen erfasst und diese mit einer binären Operation (z.B. ähnlichkeitsbasierten Joins) verknüpft.

Für ähnlichkeitsbasierte Anfragen ist natürlich das Bild selbst das wichtigste Objekt in der Bildtabelle. Der Signaturvektor und die anderen Attribute, die es näher beschreiben, sind vom jeweiligen Bild abhängig.

Auto PC

Auto PDA_Phone

Eine ähnlichkeitsbasierte Algebra

1

Inhaltsbasierte Retrieval-Methoden

k-NN424:
für i = 1,...,k
und

Bereichsanfrage:

wobei |o'-q| die Distanz zwischen o' und q beschreibt.

Inhaltsbasierte Retrieval-Methoden

Ähnlichkeitsbasierte Operatoren für Bilddatenbanken

Ein ähnlichkeitsbasierter Selektionsoperator

• Ist ein unärer Operator in einer Bildtabelle M, ausgeführt auf der Komponente f,
• Gegeben ist ein Bildanfrageobjekt x, eine Bildtabelle M und ε >0;
• Def: wobei die Bereichsanfrage bezüglich ε beschreibt, mit dem Anfragebild x und der Menge der Bilder in der Bildtabelle M.

Ein ähnlichkeitsbasierter Join-Operator

• Ein binärer Operator in Bildtabellen, ausgeführt auf f,
• für M1(id1, O1, F1, A1, P1) und M2(id2, O2, F2, A2, P2); ε >0

Auto PC

Auto PDA_Phone

Auto

Proble ist nicht symmetrisch

Bedarf für einen "symmetrischen ähnlichkeitsbasierten Join-Operator"
z.B. Anfrageoptimierung

Additive Vereinigung

M1(id1, O1, F1, A1, P1) und M2(id2, O2, F2, A2, P2) sind zwei Bildtabellen.

Die Additive Vereinigung von M1 und M2 wird definiert als:

Symmetrischer ähnlichkeitsbasierter Join-Operator

Auto PC

Auto PDA_Phone

Auto

Eigenschaft: ist symmetrisch

Der Mine-Operator

• Mine (M1M2) = M2M1
• Mine (M2M1) = M1M2
  • Er verwendet die Komponente P1 von M1M2 und baut daraus M2M1.
• Die Kosten von der Mine-Operation sind vernachlässigbar verglichen mit ähnlichkeitsbasierten Operationen,
• Mine ist ein Operator, der die Vorteile der Bereichsanfrage ausnützt

Vorteil:

• Wenn M1M2 vorhanden ist, kann M2M1 mit weniger Kosten berechnet werden
• Sehr nützlich für die Anfrageoptimierung
  (ein Anfrageoptimierer kann auswählen, ob er zuerst M1M2 oder M2M1 berechnet - je nach Kosten - und mit dem Mine-Operator die jeweils andere erzeugen)

Auto PC

Auto PDA_Phone

Andere relevante ähnlichkeitsbasierte Operatoren

• Mehrfacher ähnlichkeitsbasierter Join
• Gegeben sind die zwei Bildtabellen, M1 und M2:
  • Asymmetrischer ähnlichkeitsbasierter Durchschnitt () ,
  • Asymmetrische ähnlichkeitsbasierte Vereinigung (),
  • Ähnlichkeitsbasierte Differenz (-²),
  • Kartesisches Produkt von zwei Bildtabellen
• Gegeben ist eine relationale Tabelle R und eine Bildtabelle M:
  • Relationale Selektion auf eine Bildtabelle,
  • Ein relationaler Join zweier Bildtabellen,
  • Ein relationaler Join zwischen einer Bildtabelle und einer relationalen Tabelle

2

Inhaltsbasierte Retrieval-Methoden

Im Folgenden sind eine ähnlichkeitsbasierte Algebra eingeführt, welche es einem Datenbanksystem ermöglicht, Multimedia-Anfragen abzuarbeiten und zu optimieren. Der erste Operator der Algebra ist der ähnlichkeitsbasierte Selektionsoperator, der auf der k-Nächsten-Nachbar-Suche basiert. Diese Suche liefert k Bilder zurück, die einem Anfragebild q am ähnlichsten sind. Die Nächste-Nachbar-Suche ist wie folgt definiert:

für i = 1,...,k
und wobei S die Menge der Bilder darstellt und |o'-q| die Distanz zwischen o' und q beschreibt, und die Bilder in der Ergebnismenge die geringste Distanz zum Anfragebild q aufweisen müssen. Eine ähnlichkeitsbasierte Bereichsanfrage auf einer Menge von Bildern S gibt diejenigen Bildobjekte zurück, die sich innerhalb einer bestimmten Distanz ε vom Anfragebild q befinden. Eine Bereichsanfrage kann formal wie folgt definiert werden:

wobei |o'-q| die Distanz zwischen o' und q beschreibt. Wenn man die k-Nächste-Nachbar-Suche mit der Bereichsanfrage vergleicht, zeigt sich, dass bei der k-NN424-Suche die Anzahl der zurückgegebenen Bilder k ist, bei der Bereichsanfrage hingegen ist die Anzahl ε -abhängig. Das Ermitteln der Werte von k und ε ist bei der k-NN424-Suche einfach, bei der Bereichsabfrage nicht. Dafür sind hier symmetrische Join-Operationen möglich, außerdem hat man den Vorteil der Optimierung. Das ist bei der k-NN424-Suche nicht der Fall.

Inhaltsbasierte Retrieval-Methoden

Ähnlichkeitsbasierte Operatoren für Bilddatenbanken

Ein ähnlichkeitsbasierter Selektionsoperator

Für ähnlichkeitsbasierte Anfragen in Bilddatenbanken können mehrere Operatoren verwendet werden. Der erste Operator, der hier behandelt wird, ist der ähnlichkeitsbasierte Selektionsoperator, ein unärer Operator in einer Bildtabelle M, der auf einer Komponente f, dem Signaturvektor, ausgeführt wird. Dieser lässt sich formal wie folgt definieren: Gegeben sei ein Bildanfrageobjekt x mit dem Signaturvektor, eine Bildtabelle M und ε > 0 . Die ähnlichkeitsbasierte Selektion ist dann definiert als:

• Def: wobei die Bereichsanfrage bezüglich ε beschreibt, mit dem Anfragebild x und der Menge der Bilder in der Bildtabelle M. Dieser Operator verwendet also die Bereichsanfrage, um die ähnlichsten Bilder zum Anfragebild x zu finden. Danach werden diejenigen Tupel der Bildtabelle M zurückgegeben, deren Bildobjektkomponenten ähnlich zum Anfragebild x sind.

Ein ähnlichkeitsbasierter Join-Operator

Ein weiterer ähnlichkeitsbasierter Operator in Bilddatenbanken ist der ähnlichkeitsbasierte Join-Operator, ein binärer Operator in Bildtabellen, der auf den Signaturvektoren f ausgeführt wird. Gegeben seien zwei Bildtabellen M1(id1, O1, F1, A1, P1) und M2(id2, O2, F2, A2, P2), und ein ε >0. Die ähnlichkeitsbasierte Join-Operation wird mit M1M2 bezeichnet und ist folgend definiert:

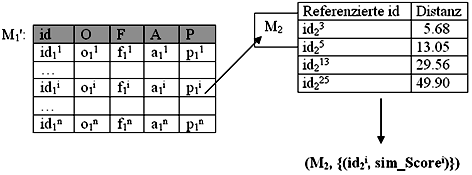
Diese Operation liefert als Ergebnis wieder eine Bildtabelle zurück, die die Einträge der Tabelle M1 mit einer veränderten Komponente P beinhaltet. P' besteht nach der ähnlichkeitsbasierten Join-Operation aus Referenzen zur Tabelle M2. Diese Referenzen beinhalten auch die Information über die Distanz zwischen den Bildobjekten. Es folgt ein Beispiel zur Erläuterung.

Auto PC

Auto PDA_Phone

Auto

Obige Abbildung zeigt die Tabelle M1', die das Ergebnis der ähnlichkeitsbasierten Join-Operation beinhaltet. Wie die Definition erkennen lässt, ist der ähnlichkeitsbasierte Join-Operator im Gegensatz zum relationalen Join-Operator nicht symmetrisch. Das heißt, dass die Reihenfolge der Bildtabellen wichtig ist. Steht eine Bildtabelle auf der linken Seite der Join-Operation, werden die Objekte dieser Tabelle als Referenz für die Ähnlichkeitsoperation verwendet.

Kommen wir noch einmal auf die Anfrage 2 am Anfang dieser LU zurück:
Für alle Bilder in Tabelle ÜB, die gestern zwischen 16:00 und 18:00 aufgenommen wurden, sollen die ähnlichsten Bilder in Tabelle MA ausgegeben werden, samt ihrer zugehörigen Namen und Adressen.

Bei dieser Anfrage sollte die Bildtabelle ÜB auf der linken Seite der ähnlichkeitsbasierten Join-Operation stehen, da wir ja zuerst daran interessiert waren, welche Personen das Gebäude betraten.

Durch die Eigenschaft, dass der ähnlichkeitsbasierte Join-Operator nicht symmetrisch ist, wird jedoch eine Anfrageoptimierung erschwert. Deshalb wird nach einem ähnlichkeitsbasierten Join-Operator mit symmetrischen Eigenschaften gesucht.

Additive Vereinigung

Um den ähnlichkeitsbasierten Join-Operator an ähnlichkeitsbasierte Anfrageoptimierung anzupassen, erweitern wir den multimedialen Join zu einem symmetrischen ähnlichkeitsbasierten Join. Dazu definieren wir zuerst einen grundlegenden Operator, nämlich die Additive Vereinigung. Die Additive Vereinigung von M1 und M2 wird definiert als:

wobei M1(id1, O1, F1, A1, P1) und M2(id2, O2, F2, A2, P2) wieder zwei Bildtabellen darstellen. Die Additive Vereinigung von M1 und M2 liefert als Ergebnis eine Bildtabelle, die alle Instanzen aus M1 und M2 enthält, und sie ist eine symmetrische Operation.

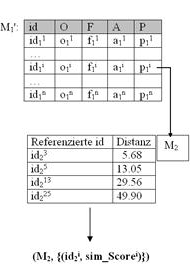
Symmetrischer ähnlichkeitsbasierter Join-Operator

Der symmetrische ähnlichkeitsbasierte Join-Operator setzt sich aus dem nicht symmetrischen ähnlichkeitsbasierten Join und der symmetrischen Additiven Vereinigung zusammen. Der symmetrische Join-Operator lässt sich wie folgt definieren, wobei M1 und M2 wieder zwei Bildtabellen darstellen:

Dieser Operator ist jetzt durch die Kombination von ähnlichkeitsbasiertem Join und Additiver Vereinigung symmetrisch.

Auto PC

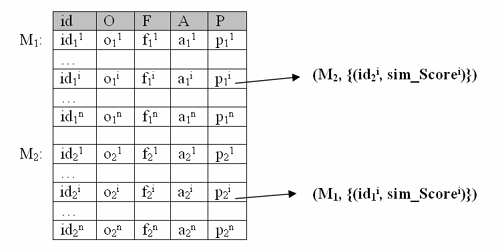
Auto PDA_Phone

Auto

In obiger Abbildung wird die Ergebnisbildtabelle dargestellt, die nach dem symmetrischen ähnlichkeitsbasierten Join aus M1 und M2 besteht. M1 und M2 beinhalten in der veränderten Komponente P die Referenzen zu Bildobjekten der jeweils anderen Tabelle.

Der Mine-Operator

Das Ergebnis eines symmetrischen ähnlichkeitsbasierten Joins ist die Additive Vereinigung von M1M2 und M2M1. Durch die Verwendung eines zusätzlichen Operators kann der symmetrische Join mit geringeren Kosten berechnet werden. Dieser Operator heißt Mine. Folgende Vorgangsweise ist möglich: Zuerst wird nur einer der beiden einseitigen Joins mit dem ähnlichkeitsbasierten Join-Operator berechnet. Die zweite Ergebnistabelle kann nachträglich durch den Mine-Operator erzeugt werden. Die formale Definition des Mine-Operators lautet:

Mine (M1M2) = M2M1
Mine (M2M1) = M1M2

Der Operator verwendet die Komponente P1 von M1M2 und baut daraus die Tabelle M2M1. Der Vorteil ist, dass die Kosten verglichen mit ähnlichkeitsbasierten Operationen vergleichbar gering sind, und so vernachlässigt werden können. Ist nun die Tabelle M1M2 vorhanden, kann M2M1 mit viel weniger Kosten berechnet werden, als der symmetrische ähnlichkeitsbasierte Join verursachen würde. Das ergibt einen großen Vorteil für die Anfrageoptimierung. Ein Anfrageoptimierer kann nun beispielsweise auswählen, ob er nun zuerst M1M2 oder M2M1 berechnet, je nachdem, welche Join-Operation mehr Kosten verursacht. Mit dem Mine-Operator kann danach die jeweils andere Tabelle kostengünstig erzeugt werden. Der Mine-Operator nützt die Vorteile der Bereichsanfrage aus (siehe folgender Abschnitt). Die folgende Abbildung soll die Arbeitsweise des Mine-Operators näher erklären:

Auto PC

Auto PDA_Phone

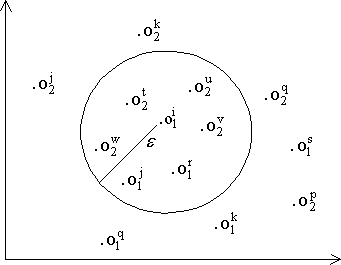
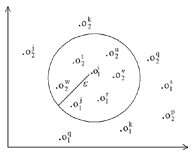
Auto

Obige Abbildung stellt eine Repräsentation der Bilddatenpunkte von M1 und M2 dar (zu Visualisierungszwecken im zweidimensionalen Raum). Durch die ähnlichkeitsbasierte Join-Operation M1M2 wird eine Bereichsanfrage durchgeführt. Ausgehend von einem Objekt o1i in M1 sucht die Bereichsanfrage alle Objekte o2 aus M2, die innerhalb einer gewissen Distanz ε vom Anfrageobjekt liegen. Es werden also die Objekte o2^t, o2^u, o2^v und o2^w ausgewählt. Durch den Multimedia-Join werden diese Ergebnisobjekte in der Komponente P der Ergebnistabelle als Referenz gespeichert.
Nun sieht man, dass bei der Berechnung von M2M1 mit dem ähnlichkeitsbasierten Join für o2^t, o2^u, o2^v und o2^w, also jedes Ergebnisobjekt aus M2, genau die Ausgangsobjekte o1^i zurückgeliefert werden, da die Distanz ε symmetrisch ist. Diese Information ist aber schon in der Komponente P aus M1M2 vorhanden und könnte verwendet werden. Werden alle P-Komponenten aus M1M2 betrachtet, können alle Instanzen aus M2M1 erzeugt werden. Der Algorithmus des Mine-Operators kann diese Eigenschaft verwenden.

Andere relevante ähnlichkeitsbasierte Operatoren

Ein weiterer relevanter ähnlichkeitsbasierter Operator, ist beispielsweise der mehrfache ähnlichkeitsbasierte Join M1M2... Mn, der mehrere Tabellen miteinander verknüpft. Da diese Operation nicht symmetrisch ist, spielt natürlich die Reihenfolge der Tabellen eine Rolle. Um Symmetrie zu erhalten muss der Operatorverwendet werden.

Wenn zwei Bildtabellen M1 und M2 gegeben sind, können folgende Operationen durchgeführt werden:

• Asymmetrischer ähnlichkeitsbasierter Durchschnitt ()
• Asymmetrische ähnlichkeitsbasierte Vereinigung ()
• Ähnlichkeitsbasierte Differenz (-²)
• Kartesisches Produkt von zwei Bildtabellen

Ist eine relationale Tabelle R und eine Bildtabelle M gegeben, kann man folgende Operationen definieren:

• Eine relationale Selektion auf einer Bildtabelle
• Einen relationalen Join zweier Bildtabellen
• Einen relationalen Join zwischen einer Bildtabelle und einer relationalen Tabelle

Nähere Details zu den Operationen findet man in: ABK01

Bibliographie

2

Auto

ABK01