zu große Graphiken ausgebessert

Acronyme, Absätze, Wordanführungszeichen done.

Review von Prof. Kosch eingearbeitet.

Unbekannte Character removed.

Formeln inline gesetzt.

Traditionelle Optimierungstechniken

1

Anfrageoptimierung in traditionellen Datenbanken

Reihenfolge der Joins auswählen

Auto PC

Auto PDA_Phone

Dynamische Programmierung

Berechnung des besten Plans für alle Teilmengen der Relationen

Auto PC

Auto PDA_Phone

Auto

• Selektionen und Projektionen so weit wie möglich in Richtung der Blätter verschieben
• Für jeden Join die Reihenfolge der Operatoren und den möglichen Austausch mit anderen Joins untersuchen!
• Reihenfolge der gejointen Tabellen
  • Join könnte durch Sortierung der Inputtabellen nach Join-Attributen billiger sein
• Kostenbasierte Optimierung
  • Kosten für Joins und Selektionen sind wohldefiniert: CPU352 + I/O Kosten
  • Schätzen der Größe von Zwischenrelationen durch Stichproben/Histogramme
• Heuristische und randomisierte Optimierungsstrategien (z.B. Iterative Improvement)

Optimierung in Multimediadatenbanken

• Teure Prädikate/Funktionen in Selektionen/Projektionen/Joins
  • Anfragen basierend auf der Manipulation von Bildern oder Ähnlichkeitssuche
  • Ist eine Selektion teurer als ein Join oder nicht?
• Übliche Heuristik ("Selektionen werden soweit wie möglich in Richtung der Blätter verschoben") funktioniert gewöhnlich nicht.

2

Anfrageoptimierung in traditionellen Datenbanken

Die Anfrageoptimierung in traditionellen Datenbanken gliedert sich in verschiedene Optimierungsklassen. Eine wichtige Klasse ist die Auswahl der Reihenfolge der Joins.

Auto PC

Auto PDA_Phone

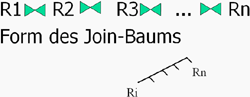
Auto

Obige Abbildung zeigt einen n-fachen Join von Relationen. Die Reihenfolge der Ausführung der einzelnen Joins kann in einem sogenannten Join-Baum graphisch dargestellt werden. Die Form des Baums spielt dabei eine entscheidende Rolle. Um die beste Form zu bestimmen setzt man die dynamische Programmierung ein. Dadurch kann eine optimale Reihenfolge für das Joinen der Tabellen ermittelt werden, indem der beste Plan für alle Teilmengen der Relationen berechnet wird.

Auto PC

Auto PDA_Phone

Auto

In obiger Abbildung wird die rekursive Formel für einen besten Plan von n Relationen dargestellt. Als Ergebnis wird die Reihenfolge der Relationen zurückgeliefert, durch welche die entstehenden Kosten beim Joinen minimal sind. Eine sehr wichtige Regel bei der traditionellen Anfrageoptimierung ist es, die Selektionen und Projektionen so weit wie möglich in Richtung der Blätter des Anfragebaums zu verschieben. Außerdem sollte man die Reihenfolge der Operatoren und den möglichen Austausch mit anderen Joins untersuchen. Die Reihenfolge der verwendeten Tabellen im Join ist generell ein wichtiger Punkt, der überprüft werden sollte. Ein Join könnte durch die Sortierung der Inputtabellen nach Join-Attributen wesentlich weniger Kosten verursachen.

Die Anfrageoptimierung wird kostenbasiert durchgeführt. Für die Berechnung der Kosten von Joins und Selektionen können wohldefinierte CPU352- bzw. I/O-Kosten verwendet werden. Die Größe von Zwischenrelationen basieren auf Schätzungen durch Stichproben oder Histogrammen. Für komplexere Anfragen verzichtet man auf dynamische Programmierung, sondern setzt heuristische und randomisierte Optimierungsstrategien, wie zum Beispiel Iterative Improvement, ein.

Optimierung in Multimediadatenbanken

Anfragen in multimedialen Datenbanken können sich sehr von Anfragen in traditionellen Datenbanksystemen unterscheiden. Anfragen können multimediale Objekte beinhalten, die vom Benutzer als Input eingegeben werden. Es werden teure Prädikate oder Funktionen in Selektionen, Projektionen und Joins verwendet, da diese Operationen oft auf der Manipulation von Bildern oder Ähnlichkeitssuchen basieren. Da auch die Extrahierung von Bildeigenschaften und ähnlichkeitsbasierte Retrieval-Algorithmen sehr teuer sind, ist es gerade in Multimediadatenbanken unabdingbar, eine Anfrageoptimierung durchzuführen.
Bei Optimierungen in multimedialen Datenbanken kann man sich oft nicht an Heuristiken traditioneller Datenbanken halten. Durch multimediale ähnlichkeitsbasierte Operationen beispielsweise kann man nicht immer davon ausgehen, dass Selektionen teurer als Joins sind. Deshalb funktioniert die übliche Heuristik, Selektionen soweit wie möglich in Richtung der Blätter zu verschieben, gewöhnlich nicht.

Probleme bei der Multimedia Anfrageoptimierung

1

Anfrageoptimierung: Join-Baum

Typische Fragen:
Soll M1 der linke oder rechte Input des Joins sein?

Auto PC

Auto PDA_Phone

2

Anfrageoptimierung: Join-Baum

Auto PC

Auto PDA_Phone

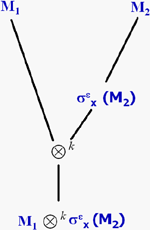
Auto

Obige Abbildung zeigt ein Beispiel eines Join-Baums mit zwei Bildtabellen M1 und M2, wobei vor dem Join von M1 mit M2 eine ähnlichkeitsbasierte Selektion auf M2 durchgeführt werden soll. In MM-Datenbanken ergibt sich typischerweise die Frage, ob M1 auf der linken oder rechten Seite des Joins stehen soll. Wenn der ähnlichkeitsbasierte Join asymmetrisch ist und die Reihenfolge der Tabellen eine semantisch Bedeutung hat kann eine Optimierung natürlich gar nicht durchgeführt werden. Ist der multimediale Join jedoch symmetrisch, kann man durch Ermitteln der Kosten von M1M2 bzw. M2M1 entscheiden, welche Inputtabelle auf welcher Seite des Joins stehen soll. Diese Entscheidung kann jedoch nur fallspezifisch getroffen werden.

Algebraische Transformationsregeln für die Anfrageoptimierung

1

Auto

• Algebraische Transformationsregeln:
  • Selektionen und Joins

• Joins
  • 

2

Auto

Um Anfrageoptimierungsstrategien in Multimediadatenbanksystemen zu entwickeln, wird eine wohldefinierte Algebra für ähnlichkeitsbasierte Operationen benötigt. Die Eigenschaften ähnlichkeitsbasierter Operatoren können dazu verwendet werden, Regeln für die Anfrageoptimierung zu entwickeln. Für die Vertauschung von Selektionen und Joins können folgende algebraische Transformationsregeln angewendet werden:

Durch die Anwendung der obigen Formeln kann eine Anfrageoptimierung erreicht werden. Bei ähnlichkeitsbasierten Joins kann erst nach einer separaten Berechnung jeder Alternative entschieden werden, welche Strategie angewendet werden soll. Die Transformationsregel M1M2 -> Mine(M2M1) spielt hierbei eine zentrale Rolle. Die Transformation sollte nur dann angewendet werden, wenn Kosten(M1M2) > Kosten(M2M1) + Kosten(Mine(M2M1)). Verglichen mit den beträchtlichen Kosten der Berechnung einer asymmetrischen Join-Operation, kann man die Kosten der Mine-Operation vernachlässigen. Darum gilt in der Praxis, dass Mine(M2M1) durchgeführt werden soll, wenn Kosten(M1M2) > Kosten(M2M1).

Bbiliographie

2

Auto

ABK01