Referenzen nächste Folie gelöscht

Acronyme, Absätze, Wordanfürhungszeichen done.

Review von Prof. Kosch eingearbeitet.

Unbekannte Character removed.

Einleitung

1

Auto

• Inhaltsbasiertes Retrieval in Multimedia Datenbanksystemen basiert auf der Verwendung von Signaturvektoren
• Low-level Merkmale eines Bildes (zB. Farbverteilungen) werden durch Signaturvektoren beschrieben
• Signaturvektoren werden aus den Daten selbst berechnet (siehe LU Ähnlichkeitsabfragen und Demosysteme).

Signaturvektoren

Beispiel für einen Signaturvektor:
Grauwert-Histogramm eines Bildes

Auto PC

Auto PDA_Phone

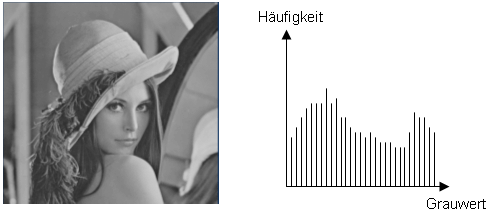
2

Auto

Für das inhaltsbasierte Retrieval in multimedialen Datenbanksystemen werden Signaturvektoren verwendet, die den Bildinhalt repräsentieren. Dabei werden Low-level Merkmale (wie zum Beispiel Farbverteilungen, Textur oder ähnliches) durch einen Signaturvektor beschrieben. Die Signaturvektoren werden dabei aus den Bilddaten selbst berechnet (siehe LU Ähnlichkeitsabfragen und Demosysteme).

Signaturvektoren

Ein Beispiel für einen Signaturvektor wäre etwa ein Grauwert-Histogramm eines Schwarz-Weiß-Bildes. Hier werden die Grauwertverteilungen im Bild dargestellt.

Auto PC

Auto PDA_Phone

Auto

Die obige Abbildung zeigt, wie die Grauwerte eines Schwarz-Weiß-Bildes als Histogramm dargestellt werden können. Diese Werte können dann im Signaturvektor gespeichert werden.

Erstellen von Indexstrukturen

1

Auto

Auto PC

Auto PDA_Phone

Dimensionsreduktion

• Ziel: Signaturvektor mit weniger Dimensionen
• aber Erhaltung der Distanz
• Warum?: Effizienz der Indexstrukturen nimmt mit Höhe der Dimensionen ab
• Mittel:
  • Transformationen
  • Raumfüllende Kurven

Dimensionsreduktion durch Transformationen

• Änderung der Basis der Vektoren
• Überführung in orthonormale Vektoren
• nach Transformation Unterscheidung von Koeffizienten mit großem und geringem Einfluß möglich
• die unwichtigen werden entfernt
• daraus entsteht ein Signaturvektor mit weniger Dimensionen

Verschiedene Transformationstechniken

Dimensionsreduktion durch raumfüllende Kurven

• Mehrdimensionaler Raum wird durch eine einzige Kurve dargestellt
• Dadurch Verwendung einer eindimensionalen Indexstruktur möglich
• Beispiele:
  • Hilbert-Kurve
  • Z-Ordering

Auto PC

Auto PDA_Phone

2

Auto

Auto PC

Auto PDA_Phone

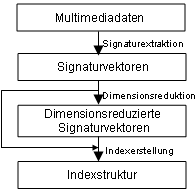
Auto

Obige Abbildung zeigt den Weg der Erstellung von Indexstukturen, der von den Multimediadaten zur Indexstruktur führt. Aus den Multimediadaten werden die low-level Merkmale extrahiert (Signaturextraktion) und in Signaturvektoren gespeichert. Diese Signaturvektoren haben unter Umständen eine hohe Dimension, die von der Genauigkeit der Extraktionsalgorithmen abhängt. Wenn z. B. für ein Farbhistogramm 1024 Werte gewählt werden, und jeder Wert durch 8 bit repräsentiert wird, nimmt ein Vektor einen Speicherbereich von 1 KB ein, was für eine große Datenbank sehr viel ist. Deswegen ist es angebracht, eine distanzerhaltende Dimensionsreduktion durchzuführen (siehe nächster Abschnitt). Bei geringen Dimensionen kann die Dimensionsreduktion sicherlich entfallen.
Aus den dimensionsreduzierten Signaturvektoren wird dann die Indexstruktur erstellt, indem zum Beispiel bestimmte Schlagwörter oder eine kurze textuelle Zusammenfassung eingesetzt werden, die den multimedialen Inhalt beschreiben.

Dimensionsreduktion

Die steigenden Ansprüche in Applikationen fordern, immer komplexere Signaturvektoren speichern zu können, die hohe Dimensionen haben können. Das Ziel der Dimensionsreduktion ist es, einige nicht signifikante Dimensionen zu verschmelzen, um so die Höhe zu verringern. Trotzdem soll die Distanz erhalten bleiben, das heißt alle Punkte sollten eine ähnliche Nachbarschafts- oder Distanzbeziehung wie vor der Transformation haben. Eine Dimensionsreduktion wird deswegen durchgeführt, weil die Effizienz der Indexstrukturen mit der Höhe der Dimensionen abnimmt.
Eine Reduktion der Dimensionen von Signaturvektoren kann entweder durch Transformationstechniken oder die Anwendung raumfüllender Kurven erreicht werden.

Dimensionsreduktion durch Transformationen

Um durch Transformation eine Reduktion der Dimensionen von Signaturvektoren zu erreichen, muss die Basis der Vektoren geändert werden. Das geschieht, indem sie in orthonormale Vektoren übergeführt werden. Diese Überführung kann mit einer mathematischen Prozedur (z. B.: Gram-Schmidt) durchgeführt werden, in der eine orthonormale Basis für den Vektorraum gesucht wird. Nach dieser Transformation besteht nun die Möglichkeit, in den orthonormalen Vektoren mathematisch zu überprüfen, welche Koeffizienten für diesen Vektorraum von Bedeutung sind, und welche weniger. Je nach Art der Daten wird hier eine andere Methode verwendet (siehe nächster Abschnitt). So kann man wichtige und unwichtige Dimensionen unterscheiden, indem man ihre Wichtigkeit und ihren Einfluss (großer Einfluss, geringer Einfluss) betrachtet. Da die unwichtigen Koeffizienten mit nur geringem Einfluss auf den gesamten Vektorraum nun herausgefiltert und entfernt werden können, entsteht ein Signaturvektor mit weniger Dimensionen.

Verschiedene Transformationstechniken

Auto

In obiger Tabelle werden die verschiedenen Techniken der Transformation und ihre Anwendungsgebiete dargestellt.

Die Karhunen-Loeve-Transformation wird verwendet, wenn geclusterte Daten vorhanden sind. Fourier bzw. FFT wird bei periodischen Daten angewendet, Wavelet bei unstetigen Daten und die DCT419 (Diskrete Cosinus Transformation) bei lokal korrelierenden Daten.

Dimensionsreduktion durch raumfüllende Kurven

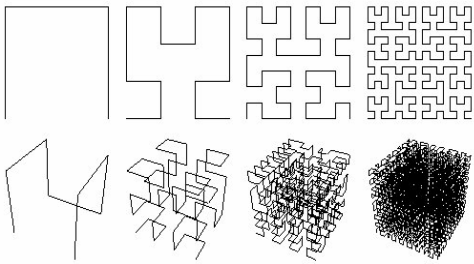
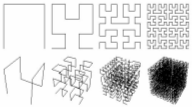
Das zweite Mittel, um die Dimensionen der Signaturvektoren reduzieren zu können, geschieht durch die Anwendung raumfüllender Kurven. Bei dieser Vorgehensweise versucht man, den mehrdimensionalen Raum durch eine einzige Kurve darzustellen. Dadurch wird dann die Verwendung einer eindimensionalen Indexstruktur möglich.
Beispiele für raumfüllende Kurven sind Hilbert-Kurven und Z-Ordering.

Hilbertkurven sind rekursiv definierte raumfüllende Kurven, die sich zur Parametrisierung mehrdimensionaler Datensätze verwenden lassen.

Auto PC

Auto PDA_Phone

Auto

In dieser Abbildung sieht man die Hilbert-Kurven H1 bis H4 im zweidimensionalen Raum (oben) und im mehrdimensionalen Raum (unten). Für den eindimensionalen Raum gilt, dass jede Hilbertkurve links unten beginnt und rechts unten endet. H1 besteht aus drei geraden Strichen, H2 setzt sich aus vier Kurven H1 und 3 geraden Verbindungsstrichen zusammen. Für jede weitere Hilbertkurve Hn gilt, dass sie aus vier Kurven Hn-1 und 3 Verbindungsstrichen besteht, wobei von den vier Kurven Hn-1 jeweils zwei nach links orientiert sind, und die beiden anderen nach rechts.

Überblick über Indexstrukturen

1

Mehrdimensionale Indexstrukturen

• R-Baum und seine Varianten sind die effektivsten Indexbäume für mehrdimensionale Indexstrukturen.
• R-Baum ist eine Verallgemeinerung des B-Baums für mehrdimensionale Räume
• jeder Knoten wird durch ein MBR418 (Minimum Bounding Rectangle) beschrieben
• Ein MBR418 enthält alle Objekte innerhalb eines Knotens (Signaturvektoren und Teilbäume)

R-Baum

Auto PC

Auto PDA_Phone

Auto

• Überlappende MBR418s bei R-Bäumen reduzieren Effizienz
• Varianten des R-Baum:
  • R+-Baum
  • R*-Baum
  • SS-Baum
  • SR-Baum
  • TV-Baum
  • X-Baum

R+ - Baum

• im R+-Baum kein Überlappen der MBR418s erlaubt
• Einfügen des Objektes in alle Knoten, deren MBR418 es überlappt
• verbessertes Suchverhalten (gegenüber R-Baum)
• Höhe des Baums ist größer als beim R-Baum

R* - Baum

• Überlappen der MBR418s erlaubt
• effizienter als R-Baum
• Grund: geänderte Einfüge- und Teilungsstrategien
• Überlauf eines Knotens: erzwungenes Wiedereinfügen
• Splitalgorithmus wird nicht sofort aufgerufen, stattdessen: versuche bestehende Einträge zu entfernen und neu einzufügen

SS-Baum

• R*-Baum und SS-Baum sehr ähnlich
• Bounding box ist ein Kreis
• Der Baum wird beim Einfügen durch ähnliche Kreisschwerpunkte geordnet
• Bessere Performanz als der R*-Baum

SR-Baum

• Erweiterung des R*-Baums und des SS-Baums
• Bounding box ist eine Kombination von Rechtecken (vgl. R*-Baum) und Kreisen (vgl. SS-Baum)
• Aufteilung der Objekte in kleinere Regionen, die dadurch disjunkter sind
• Effizientes Suchen
• Details (siehe LU Fallbeispiel: SR-Bäume)

TV-Baum

• Variierende Anzahl von Dimensionen zur Indizierung
• Verwendete Dimensionen abhängig von:
  • Anzahl der zu indizierenden Objekte
  • aktuelle Baumhöhe
• Knoten nah an der Wurzel: Betrachtung weniger Dimensionen
• Zu verwendende Dimensionen werden durch Teleskop-Funktion berechnet
• Überlappungen erlaubt -> Probleme bei Knoten die unterschiedliche Dimensionen zur Indizierung benutzen
• weiteres Problem: ersten Dimensionen enthalten oft den gleichen Wert

X-Baum

• eXtended tree
• Splitting wird möglichst vermieden
• möglich durch Superknoten -> doppelte Kapazität eines "normalen" Knotens
• Splitting anhand Splithistorie -> findet Split mit minimaler Überlappung
• effizienter als TV-Baum und R*-Baum

2

Mehrdimensionale Indexstrukturen

Herkömmliche Indexstrukturen wie B-Bäume können lediglich eindimensionale Daten speichern und suchen. In vielen Anwendungsgebieten gewinnen jedoch auch mehrdimensionale Daten an Bedeutung. Die Anforderungen an Indexstrukturen, die auch mit mehrdimensionalen Daten arbeiten können, steigen. Am effektivsten für mehrdimensionale Räume haben sich der R-Baum und seine verschiedenen Varianten gezeigt.
Der R-Baum ist eine Verallgemeinerung des B-Baums. Es handelt sich dabei um eine dynamische Indexstruktur, Daten können also jeder Zeit in einen bestehenden Baum eingefügt, verändert oder gelöscht werden. Der R-Baum ist balanciert, seine Knotengröße ist auf die Seitengröße abgestimmt. Die räumlichen Daten werden mit Hilfe von minimal umgebenden Rechtecken - Minimum Bounding Rectangle (MBR418) strukturiert. Es handelt sich dabei um Rechtecke, die jedes Datenobjekt minimal umspannen. Jeder Knoten des R-Baums wird durch ein MBR418 beschrieben, das alle Objekte innerhalb eines Knotens, wie Signaturvektoren und Teilbäume, enthält. In R-Bäumen dürfen MBR418s einander schneiden, ein Objekt darf aber nur in einem MBR418 gespeichert werden.

R-Baum

Auto PC

Auto PDA_Phone

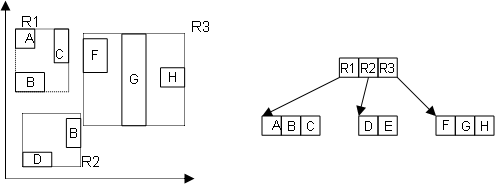
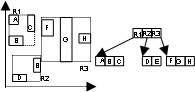
Auto

Mit Hilfe der Abbildungen R-Baum (a) und (b) soll der Aufbau des R-Baumes näher betrachtet werden.
Die Datenstruktur des R-Baums besteht aus so genannten Directory- und aus Datenseiten. Die Rechtecke R1, R2 und R3 stellen die Directoryseiten dar. Sie repräsentieren die inneren Knoten des Baumes, in denen Directory-Einträge gespeichert werden.
A, B und C sind die Datenseiten, die auf der Directoryseite R1 liegen. Jede Datenseite speichert ein Datenobjekt und ist einer Directoryseite zugeordnet. Die Datenseiten entsprechen den Blattknoten des Baumes und speichern räumliche Daten wie zum Beispiel geclusterte Punktdaten oder n-dimensionale Datenobjekte. Diese räumlichen Daten werden mit den vorher beschriebenen MBR418s strukturiert.

Es können wie beim B-Baum verschiedene Operationen ausgeführt werden. Das Suchen, Einfügen und Löschen eines Datenobjektes geschieht analog zum B-Baum.

In R-Bäumen sind Überlappungen der MBR418s erlaubt, dadurch steigen die Kosten der Seitenzugriffe und die Effizienz wird reduziert. Aus diesem Grund ist es erforderlich, Überlappungen zu vermeiden bzw. minimal zu halten. Vermeidung wäre beim R-Baum allerdings nur möglich, wenn die Überlappungen aller Datenpunkte im voraus bekannt wären. Da aber der R-Baum eine dynamische Indexstruktur ist, ist dies in der Praxis nicht der Fall. Da vor allem in hochdimensionalen Räumen das Hauptproblem des R-Baumes die vielen Überlappungen (bis zu 90%) sind und damit verbunden eine schlechte Performance, wurde eine Reihe von Varianten des R-Baums entwickelt, auf die im Folgenden näher eingegangen wird:

• R+-Baum
• R*-Baum
• SS-Baum
• SR-Baum
• TV-Baum
• X-Baum

R+ - Baum

Beim R+-Baum, einer Erweiterung zum R-Baum, sind Überlappungen der MBR418s nicht erlaubt. Wenn es zu einer Überlappung kommt, wird das Objekt in alle Knoten, deren MBR418 es überlappt, eingefügt. Der Eintrag ist dann einfach in mehreren Blättern vorhanden.
Der Vorteil von R+-Bäumen ist ein verbessertes Suchverhalten gegenüber dem R-Baum. Es müssen nicht unnötig Pfade durchlaufen werden, um dann festzustellen, dass das gesuchte Datenobjekt nicht auf dem entsprechenden Knoten liegt. Vor allem bei Punktanfragen können Zugriffsersparnisse sogar mehr als 50% betragen, allerdings erfordert dies auf der anderen Seite einen höheren Speicheraufwand. Als Konsequenz haben die R+-Bäume eine größere Baumhöhe als die R-Bäume.

R* - Baum

Der R*-Baum ist eine Weiterentwicklung des R+-Baums. Er ermöglicht durch einen ausgeklügelten Splitalgorithmus eine weitere Effizienzsteigerung.
Beim R*-Baum sind Überlappungen der MBR418s erlaubt, es wird jedoch eine Optimierung angestrebt, die durch Minimierung von Überlappungen und Umfang der MBR418s erreicht wird. Dadurch wird der R*-Baum effizienter als der R-Baum. Die Optimierung wird durch einen neuen Einfügealgorithmus erreicht. Durch geänderte Einfüge- und Teilungsstrategien kann das Einfügen von neuen Datenobjekten ein Löschen und Wiedereinfügen anderer Objekte verursachen. Beim Überlauf eines Knotens wird ein Wiedereinfügen erzwungen, indem der Splitalgorithmus nicht sofort aufgerufen wird. Stattdessen wird versucht, bestehende Einträge zu entfernen und neu einzufügen. Diese Vorgangsweise führt zu einer weiteren Verkleinerung der Überlappung der MBR418s.

SS-Baum

Der SS-Baum ist dem R*-Baum sehr ähnlich. Er verwendet wie der R*-Baum eine Wiedereinfüge-Strategie, um die Überlappung der MBR418s zu verkleinern. Diese Strategie weist nur leichte Unterschiede auf. Beim SS-Baum werden anstatt den MBR418s Kreise als bounding boxes (Seitenregionen) benutzt. Beim Einfügen wird die Ähnlichkeit des Schwerpunktes eines Kreises ermittelt und so eine Ordnung im Baum erzeugt. Dies führt ebenfalls zu einer verbesserten Performanz im Gegensatz zum R*-Baum.

SR-Baum

Der SR-Baum ist eine Erweiterung des R*-Baums und des SS-Baums. Er benutzt eine Kombination aus Rechtecken und Kreisen als Seitenregion, wobei die Rechtecke aus dem R*-Baum übernommen wurden, und die Kreise aus dem SS-Baum. Durch diese Kombination können die beschriebenen Objekte in kleinere Regionen aufgeteilt werden, die dadurch disjunkter sind. Das steigert die Effizienz beim Suchen im Baum.
Der SR-Baum wird in der LU Fallbeispiel: SR-Bäume detaillierter behandelt.

TV-Baum

Der TV-Baum (Telescope Vector Baum) hat eine ähnliche Struktur wie der R-Baum und wurde speziell für Vektoren entwickelt. Er verwendet eine variierende Anzahl von Dimensionen zur Indizierung. In inneren Knoten werden die Vektoren durch niedrig-dimensionale Vektoren approximiert (eine Art Dimensionsreduktion). Dadurch soll es möglich werden, auch sehr hoch-dimensionale Daten zu indizieren. Die verwendeten Dimensionen sind abhängig von der Anzahl der zu indizierenden Objekte und von der aktuellen Baumhöhe. Bei einem Knoten, der sich nahe an der Wurzel befindet, betrachtet man weniger Dimensionen als bei Knoten, die weiter von der Wurzel entfernt sind. Die Berechnung, welche Dimensionen zu verwenden sind, wird mittels einer Teleskop-Funktion durchgeführt. Meist ist die Teleskop-Funktion so realisiert, dass sie irrelevante Teilbäume einfach abschneidet. Das erfordert eine gewisse Ordnung im Baum, wichtige Merkmale befinden sich somit näher bei der Wurzel als unwichtige. Um diese Hierarchie im Baum zu erreichen kann z. B. die Karhunen-Loeve-Transformation angewendet werden.

Beim TV-Baum sind, wie beim R*-Baum, Überlappungen erlaubt. Das kann hier aber zu Problemen bei Knoten führen, die unterschiedliche Dimensionen zur Indizierung benutzen. Ein weiteres Problem bei den TV-Bäumen ist, dass die ersten Dimensionen sehr oft den gleichen Wert enthalten, d.h. bei niedrig-dimensionalen Einträgen kann man die Vektoren nicht mehr unterscheiden.

X-Baum

Der X-Baum (eXtended tree) ist eine Weiterentwicklung des R*-Baums, bei dem Splitting möglichst vermieden werden soll. Seine Bedeutung liegt vor allem in hochdimensionalen Räumen. Es wird versucht, eine Überlappung von Knoten zu vermeiden, was speziell bei einer sehr großen Anzahl von Dimensionen problematisch werden kann. Durch Einführen von sogenannten Superknoten können diese Überlappungen vermieden werden. Die Knoten können erweitert werden und haben bis zur doppelten Kapazität eines "normalen" Knotens. Falls sich ein Split nicht lohnt, weil resultierende Knoten eine zu starke Überlappung hätten, werden die einfachen Knoten einfach zu solchen Superknoten umgewandelt, und dadurch die Kapazität erhöht werden. Anhand des verbesserten Splitting-Algorithmus wird durch eine sogenannte Splithistorie der Split mit der minimalsten Überlappung gefunden. Dadurch kann die Performance im Vergleich zum TV-Baum und zum R*-Baum deutlich verbessert werden. Der X-Baum kommt in vielen Multimedia-Datenbanksystemen zur Anwendung.

Inhaltsbasierte Anfragen

1

Auto

Auto PC

Auto PDA_Phone

Anfragearten für MMDB

• Ähnlichkeitsanfragen:
  • vorgegebenes Objekt
  • k ähnlichsten gesucht
  • Verallgemeinerung der k-Nächste-Nachbar-Suche (k-NN Suche)
  • Algorithmen entsprechen denen der NN-Suche
  • aber zusätzliche Option: Ignorieren von Knoten, mit zu großer Distanz zum Anfragevektor

• Bereichsanfragen:
  • Region gegeben
  • alle Objekte gesucht die diese schneiden
  • Verkürzung der Rechenzeit durch Ignorieren von Knoten -> Knoten, deren Schnitt mit Anfragebereich unter gegebener Schwelle liegt

Nächste-Nachbar-Suche

• Betrachtung als Bereichsanfragen
• variabler Radiuslänge
• Voraussetzung: Knoten sind durch Hüllen eingegrenzt (->MBR418)
• gegeben für R-Bäume (und Varianten)
• für schnelle Suche, schnelle Reduzierung des Radius
• Reduzierung des Radius:
  • noch nicht besuchte Knoten in Prioritätswarteschlange einordnen
  • Knoten an erster Stelle zuerst untersuchen
• Ordnung der Priorität nach:
  • minimaler Abstand zwischen Anfragepunkt und Knotenschwerpunkt
  • minimaler Abstand zwischen Anfragepunkt und Knoten
  • Minimum der maximalen Distanz

2

Auto

Auto PC

Auto PDA_Phone

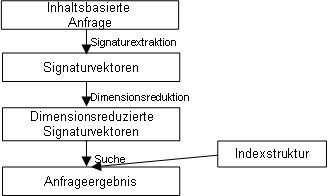
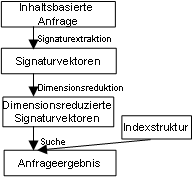
Auto

Abbildung Inhaltsbasierte Anfragen zeigt den Ablauf von der Eingabe einer inhaltsbasierten Anfrage bis zum Ergebnis der Anfrage. Es wird zuerst eine Signaturextraktion durchgeführt, wodurch wieder Signaturvektoren entstehen. Durch eine Dimensionsreduktion, falls notwendig, hochdimensionaler Vektoren entstehen dimensionsreduzierte Signaturvektoren. Mit einer bestimmten Indexstruktur kann dann die Suche ausgeführt werden und es wird das Anfrageergebnis geliefert.

Anfragearten für MMDB

Es gibt zwei verschiedene Anfragearten für Multimediadatenbanken: Ähnlichkeitsanfragen und Bereichsanfragen.
Bei Ähnlichkeitsanfragen gibt es ein vorgegebenes Objekt mit bestimmten Eigenschaften. Gesucht werden soll nach den k-ähnlichsten Objekten in der Datenbank. Die Ähnlichkeitsanfrage ist eine Verallgemeinerung der k-Nächste-Nachbar-Suche, die später in dieser LU behandelt wird. Die verwendeten Algorithmen entsprechen denjenigen, die bei der Nächste-Nachbar-Suche verwendet werden, es gibt aber eine zusätzliche Option: Knoten, die eine zu große Distanz zum Anfragevektor aufweisen, können ignoriert werden.

Die zweite Anfrageart für Multimediadatenbanken ist die Bereichsanfrage. Hier ist eine bestimmte Region mit gewissen Eigenschaften als Anfragebereich gegeben, und es werden alle Objekte gesucht, die diese Region schneiden. Als Ergebnis erhält man also alle Objekte, die die Merkmale dieser angegebenen Region aufweisen. Eine Verkürzung der Rechenzeit kann dadurch erreicht werden, dass gewisse Knoten ignoriert werden - und zwar jene, deren Schnitt mit dem Anfragebereich unter einer gegebenen Schwelle liegt.

Nächste-Nachbar-Suche

Die Nächste-Nachbar-Suche kann als Bereichsanfrage mit variabler Radiuslänge betrachtet werden. Die Voraussetzung ist, dass die Knoten durch Hüllen eingegrenzt sind (Minimum Bounding Rectangles - MBR418s). Die Nächste-Nachbar-Suche ist somit für R-Bäume und Varianten davon geeignet. Durch die Nächste-Nachbar-Suche kann die Suche sehr schnell ausgeführt werden, es wird auch eine schnelle Reduzierung des Radius erreicht.

Die Reduzierung des Radius bei der Nächste-Nachbar-Suche wird dadurch verwirklicht, indem noch nicht besuchte Knoten in eine Prioritätswarteschlange eingeordnet werden. Knoten, die an der ersten Stelle in dieser Warteschlange stehen, werden zuerst untersucht. Die Priorität wird nach verschiedenen Gesichtspunkten geordnet: Ausschlaggebend sind der minimale Abstand zwischen dem Anfragepunkt und dem Knotenschwerpunkt, der minimale Abstand zwischen dem Anfragepunkt und dem Knoten und das Minimum der maximalen Distanz.

Bibliographie

2

Auto

Kos03

LL93

BKS+90