Codeformatierung siehe LU6+7.ppt - Done, please check and remove xIgnore. Done. Review II bis auf Akronyme komplett berücksichtigt.

Acronyme, Absätze, Wordanführungszeichen done.

Review von Prof. Kosch eingearbeitet.

Unbekannte Character removed.

SR-Baum

1

Einführung

• SR-Baum420 bedeutet "Sphere/Rectangle-Baum"
• ist eine Erweiterung des R*-Baums und des SS-Baums
• Die Seitenregionen (bounding boxes) des SR-Baum420s werden durch eine Schnittmenge von Rechtecken (bounding rectangles) und Kreisen (bounding spheres) dargestellt

2

Einführung

SR-Baum420 ist eine Abkürzung für Sphere/Rectangle-Baum. Diese Indexstruktur ist eine Erweiterung des R*-Baums und des SS-Baums. Der R*-Baum verwendet Rechtecke, der SS-Baum Kreise als Seitenregionen. Das Merkmal des SR-Baum420s ist die kombinierte Verwendung von Kreisen und Rechtecken als bounding boxes. Die Seitenregionen werden durch eine Schnittmenge der bounding rectangles und bounding boxes dargestellt.

R* - Baum

1

Die Struktur des R*-Baums

Auto PC

Auto PDA_Phone

2

Die Struktur des R*-Baums

Auto PC

Auto PDA_Phone

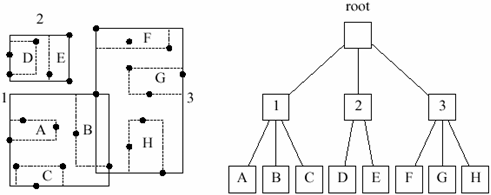
Auto

Wie Abbildungen Struktur des R*-Baums (a) und (b) zeigen, werden beim R*-Baum Rechtecke als Seitenregionen verwendet. Dabei sind Überlappungen der bounding rectangles erlaubt. Die Blattknoten im resultierenden R*-Baum beinhalten Einträge von Datenobjekten, die durch die Hierarchie des Baumes in Seitenregionen eingeteilt sind. Durch Minimierung von Überlappungen und Umfang der Seitenregionen wird eine Optimierung erreicht. Der Einfügealgorithmus im R*-Baum kann beim Einfügen neuer Datenobjekte ein Löschen und Wiedereinfügen anderer Objekte verursachen. Diese Vorgangsweise führt zu einer weiteren Verkleinerung der Überlappung der MBR418s.

SS-Baum

1

Die Struktur des SS-Baums

Auto PC

Auto PDA_Phone

2

Die Struktur des SS-Baums

Auto PC

Auto PDA_Phone

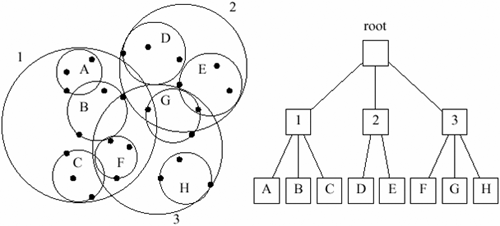
Auto

Abbildungen Die Struktur des SS-Baums (a) und (b) zeigen die Struktur des SS-Baums. Man sieht, dass im Gegensatz zum R*-Baum statt Rechtecken Kreise als Seitenregionen verwendet werden, die sich auch überlappen können. Im resultierenden SS-Baum beinhalten die inneren Knoten die Informationen aller abstammenden Knoten und verlinken so zu den Blattknoten, welche die Einträge der Datenobjekten umfassen. Beim Einfügen wird die Ähnlichkeit des Schwerpunktes eines Kreises ermittelt und eine Hierarchie im Baum erzeugt. Dadurch wird wieder eine Ordnung der Datenobjekte erreicht.

SR-Baum

1

Seitenregionen im SR-Baum

• Der Durchmesser einer Seitenregion in einem SR-Baum420 ist gleichzusetzen mit:
  • Dem Durchmesser einer bounding sphere des SS-Baums
  • Der Diagonale eines bounding rectangles des R*-Baums

Eigenschaften des SR-Baums

• Bounding rectangles gliedern die Punkte in Regionen mit kleinerem Volumen. Sie haben jedoch meist einen größeren Durchmesser als bounding spheres, vor allem in hoch-dimensionalen Räumen.
• Bounding spheres gliedern die Punkte in Regionen mit geringem Durchmesser. Sie haben jedoch meist ein höheres Volumen als bounding rectangles.
• Der SR-Baum420 kombiniert die Verwendung von bounding spheres und bounding rectangles
• Die Eigenschaften der beiden Seitenregionen sind zueinander komplementär, deshalb erlaubt ihre Schnittmenge, die Punkte in Regionen mit geringem Volumen und Durchmesser aufzuteilen

Vergleich R*-Baum, SS-Baum und SR-Baum

Vergleich R*-Baum, SS-Baum und SR-Baum

	R*-Baum	SS-Baum	SR-Baum
Form der Seitenregion
Strategie bei der Baumkonstruktion	Volumen und Überlappungen minimieren	Durchmesser	Durchmesser
Durchmesser*	4	1	1
Volumen*	60	10^9	1

Auto

* Die Werte für Durchmesser und Volumen wurden einem Test entnommen, der mit 16-dimensionalen Punktdaten durchgeführt wurde.

Die Struktur des SR-Baums

Auto PC

Auto PDA_Phone

Einfügealgorithmus

• Der Einfügealgorithmus eines SR-Baum420s basiert auf dem Algorithmus des SS-Baums, der sich auf den Schwerpunkt in den bounding spheres stützt.
• Beim Durchsuchen wird beim Herabsteigen im Baum derjenige Teilbaum ausgewählt, der den ähnlichsten Schwerpunkt zum neuen Eintrag hat.
• Im Algorithmus des SR-Baum420s werden beide Seitenregionen (bounding spheres und bounding rectangles) aktualisiert.

Löschalgorithmus

• Der Löschalgorithmus im SR-Baum420 funktioniert ähnlich wie im R-Baum
• Wenn das Löschen eines Eintrags keine Unterauslastung von Blättern/Knoten verursacht, wird er einfach entfernt
• Andernfalls werden zu wenig ausgelastete Blätter/Knoten entfernt und alle verwaisten Einträge neu eingefügt

Nächste-Nachbar-Suche im SR-Baum

• Der Algorithmus realisiert eine geordnete Tiefensuche
• Es wird eine Anzahl an Punkten gefunden, die der Anfrage am nächsten sind und ein Menge an möglichen Kandidaten gebildet
• Die Menge der möglichen Kandidaten wird überprüft, indem der Algorithmus jedes Blatt besucht, dessen Seitenregion sich mit dem Bereich der Kandidatenmenge überlappt
• Nachdem alle Blätter besucht wurden, wird der letzte Kandidat als Ergebnis der Suche zurückgeliefert.

Minimale Distanz (MINDIST)

Euklidische Distanz zwischen dem Anfragepunkt und der Seitenregion

Minimax-Distanz (MINMAXDIST)

minimaler Wert aller maximalen Entfernungen zwischen den Anfragepunkten und den jeweiligen Punkten auf allen n Achsen

Pruning bei der Suche in SR-Bäumen

• Beim Pruning werden Teilbäume, in denen sich das gesuchte Objekt nicht befinden kann, abgeschnitten und verworfen, damit sie nicht unnötig weiter durchlaufen werden.
• Eine Region R1 wird verworfen, wenn ihre MINDIST größer ist als die MINMAXDIST einer anderen Region R2, da sie den nächsten Nachbar dann nicht beinhalten kann (downward pruning)
• Wenn die tatsächliche Entfernung vom Anfragepunkt P zu einem gegebenen Objekt O größer ist als die MINMAXDIST einer Region, wird sie verworfen (upward pruning)
• Eine Region mit einer MINDIST, die größer ist als die tatsächliche Entfernung vom Anfragepunkt P zu einem Objekt O, wird verworfen (upward pruning)

Rekursive Prozedur Nächste-Nachbar-Suche (Blattknoten)

If Node.type = LEAF then
	For I := 1 to Node.count
		/* Entfernung des Punktes zur Region berechnen */
		dist := objectDist(Pt, Node.region)
		/*	ist die berechnete Entfernung kleiner als die der vorigen
			Region, wird dieses Blatt als nächster Nachbar bestimmt */
		if (dist < Nearest.dist) then
			Nearest.dist := dist
			Nearest.region := Node.region

Rekursive Prozedur Nächste-Nachbar-Suche (innere Knoten)

/* kein Blattknoten =>
	 ordne, sortiere, führe Pruning durch & besuche nächsten Knoten */

Else
	erzeugeSohnListe(Punkt, Knoten, sohnListe)
	/* Liste sortieren, damit der nächste Sohn zuerst ausgewählt werden kann */
	sortiereSohnListe(sohnListe)
	/* downward pruning durchführen */
	anzahl = pruneSohnListe(Knoten, Punkt, Nächster, sohnListe)
	For I := 1 to anzahl
		KnotenNeu := Knoten.aktuellerSohn
		/*mit nächstem Sohn der Verzweigung Suche weiterführen */
		nearestNeighborSearch(KnotenNeu, Punkt, Nächster)
		/* upward pruning durchführen */
		anzahl := pruneSohnListe(Knoten, Punkt, Nächster, sohnListe)

Stärken des SR-Baums

• SR-Baum420 teilt Punkte in Regionen mit kleinem Volumen und geringem Durchmesser auf
• Die Aufteilung der Punkte in kleinere Regionen verbessert die Disjunktheit
• Kleineres Volumen und Durchmesser erhöht die Performanz der Nächste-Nachbar-Suche

Schwächen des SR-Baums

• Hoher Aufwand bei der Erzeugung
• Die Größe der Knoten wächst, wenn die Dimensionalität größer wird
• Eine Reduzierung der Verzweigungen kann erfordern, dass bei Anfragen mehr Knoten gelesen werden müssen.
• Möglicherweise wird dadurch die Performanz bei Anfragen beeinträchtigt

2

Seitenregionen im SR-Baum

Das unterscheidende Merkmal des SR-Baum420s ist die kombinierte Verwendung von Rechtecken und Kreisen als Seitenregionen. Dabei ist der Durchmesser einer solchen Seitenregion in einem SR-Baum420 gleichzusetzen mit:

• Dem Durchmesser einer bounding sphere des SS-Baums
• Der Diagonale eines bounding rectangles des R*-Baums

Eigenschaften des SR-Baums

Entsprechend verschiedener Performancetests haben bounding rectangles und bounding spheres verschiedene Vor- und Nachteile. Bounding rectangles gliedern die Punkte in Regionen mit kleinerem Volumen. Sie haben jedoch meist einen größeren Durchmesser als bounding spheres. Das ist vor allem in hochdimensionalen Räumen der Fall. Bounding spheres hingegen gliedern die Punkte in Regionen mit geringerem Durchmesser. Sie haben jedoch meist ein höheres Volumen als bounding rectangles.Bounding rectangles haben also Vorteile in Bezug auf ihr Volumen, bounding spheres hingegen sind günstiger wenn man den Durchmesser betrachtet.

SR-Bäume nutzen die Vorteile beider Strukturen, darauf wird nun in den nächsten Abschnitten näher eingegangen.

Der SR-Baum420 nützt die Vorteile von bounding rectangles und spheres und kombiniert so die Verwendung von Rechtecken und Kreisen als Seitenregionen. Da die Eigenschaften der beiden Seitenregionen zueinander komplementär sind, erlaubt es die Schnittmenge von bounding rectangles und bounding spheres, die Punkte in Regionen mit sowohl geringem Volumen als auch geringem Durchmesser aufzuteilen. Es wurde gezeigt, dass durch diese Kombination der Strukturen, die Performanz deutlich erhöht werden konnte (vor allem bei den hochdimensionalen Daten in Bild- oder Videoanwendungen).

Vergleich R*-Baum, SS-Baum und SR-Baum

Vergleich R*-Baum, SS-Baum und SR-Baum

	R*-Baum	SS-Baum	SR-Baum
Form der Seitenregion
Strategie bei der Baumkonstruktion	Volumen und Überlappungen minimieren	Durchmesser	Durchmesser
Durchmesser*	4	1	1
Volumen*	60	10^9	1

Auto

* Die Werte für Durchmesser und Volumen wurden einem Test entnommen, der mit 16-dimensionalen Punktdaten durchgeführt wurde.

Abbildung Vergleich R*-Baum, SS-Baum und SR-Baum420 zeigt den Vergleich zwischen R*-Baum, SS-Baum und SR-Baum420. Man sieht die Form der Seitenregionen, die die Punktdaten umgeben (R*-Baum mit Rechteck, SS-Baum mit Kreis, SR-Baum420 mit der Schnittmenge von Rechteck und Kreis). Die Strategie bei der Konstruktion des Baumes beschäftigt sich beim R*-Baum mit der Minimierung des Volumens und möglichen Überlappungen, beim SS-Baum und SR-Baum420 hingegen mit der Minimierung des Durchmessers. Man erkennt außerdem, dass der Durchmesser beim R*-Baum weit größer ist, als beim SS-Baum und SR-Baum420. Ebenso ist das Volumen des SS-Baums sehr hoch, beim R*-Baum und SR-Baum420 hingegen niedriger. Die Daten von Durchmesser und Volumen wurden einem Test entnommen, der mit 16-dimensionalen Punktdaten durchgeführt wurde.

Quelle: Kat03

Die Struktur des SR-Baums

Auto PC

Auto PDA_Phone

Auto

Wie sich in den obigen Abbildungen gut erkennen lässt, basiert die Struktur des SR-Baum420s auf dem Aufbau des R*-Baums und des SR-Baum420s. Die ineinander geschachtelte Hierarchie der Seitenregionen bildet die Struktur des SR-Baum420s. Eine Seitenregion besteht aus den Punkten, die in der Schnittmenge eines Rechtecks und eines Kreises liegen, wie schon zuvor beschrieben.

Einfügealgorithmus

Der Einfügealgorithmus in einem SR-Baum420 basiert auf dem des SS-Baums, der sich auf den Schwerpunkt in den bounding spheres stützt. Dieser Algorithmus ist besonders effektiv bei Nächste-Nachbar-Suchen. Beim Durchsuchen wird beim Herabsteigen im Baum derjenige Teilbaum ausgewählt, der den ähnlichsten Schwerpunkt zu dem neuen Eintrag hat. Der einzige Unterschied zum Algorithmus im SS-Baum besteht darin, dass im SR-Baum420 nach dem Einfügen beide Seitenregionen (bounding spheres und bounding rectangles) aktualisiert werden müssen. Das Aktualisieren der bounding rectangles erfolgt gleich wie im R*-Baum, das Aktualisieren von bounding spheres unterscheidet sich jedoch von der Strategie im SS-Baum. Wie die kreisförmigen Seitenregionen aktualisiert werden, wird im nächsten Abschnitt dargestellt.

Löschalgorithmus

Der Löschalgorithmus im SR-Baum420 funktioniert ähnlich wie der im R*-Baum und im SS-Baum. Das Löschen eines Eintrags kann verursachen, dass ein Knoten nicht mehr genug ausgelastet ist, da sich zu wenig oder gar keine Einträge mehr darin befinden. Ist das der Fall, werden zu wenig ausgelastete Blätter oder Knoten entfernt und alle verwaisten Einträge neu eingefügt. Wenn das Löschen eines Eintrags keine Unterauslastung von Blättern oder Knoten verursacht, kann er einfach entfernt werden.

Nächste-Nachbar-Suche im SR-Baum

Der Algorithmus der Nächste-Nachbar-Suche im SR-Baum420 realisiert eine geordnete Tiefensuche und besteht aus zwei Phasen. In der ersten Phase wird eine Anzahl an Punkten gefunden, die der Anfrage am nächsten sind. Aus diesen Punkten wird eine Menge an möglichen Kandidaten gebildet. Die zweite Phase beschäftigt sich mit der Überprüfung dieser Menge an möglichen Kandidaten, indem der Algorithmus jedes Blatt besucht, dessen Seitenregion sich mit dem Bereich der Kandidatenmenge überlappt. Dabei wird der Baum von oben nach unten in einem tiefenorientierten Suchverfahren durchlaufen. In jedem besuchten Knoten wird die Entfernung des Anfragepunkts zur Region jedes Sohnes berechnet, wobei der Sohn mit der geringsten Distanz vor den anderen Söhnen besucht wird. Nachdem alle Blätter besucht wurden, wird der letzte Kandidat als Ergebnis der Suche zurückgeliefert.

Minimale Distanz (MINDIST), Minimax-Distanz (MINMAXDIST)

Für die Durchführung der Nächste-Nachbar-Suche in SR-Bäumen werden zwei Entfernungen betrachtet: Die minimale Distanz und die Minimax-Distanz. Die Minimale Distanz (MINDIST) wird als euklidische Distanz zwischen dem Abfragepunkt und der behandelten Seitenregion berechnet. Die Minimax-Distanz (MINMAXDIST) ist der minimale Wert aller maximalen Entfernungen zwischen den Anfragepunkten und den jeweiligen Punkten auf allen n Achsen. Durch die Berechnung der MINDIST und der MINMAXDIST beim Ermitteln des nächsten Nachbarn kann die Entfernung zwischen den Anfragepunkten und den Region besser abgeschätzt werden.

Abbildung Nächste-Nachbar-Suche zeigt graphisch den Ablauf der Nächste-Nachbar-Suche im dreidimensionalen Raum. Ausgehend vom Anfragepunkt P wird die minimale Distanz (MINDIST) und die Minimax-Distanz (MINMAXDIST) zur Seitenregion gemessen.

Pruning bei der Suche in SR-Bäumen

Die Suche in SR-Bäumen kann durch Pruning erheblich beschleunigt werden. Beim Pruning werden Teilbäume, in denen sich das gesuchte Objekt nicht befinden kann, abgeschnitten und verworfen, damit sie nicht unnötig weiter durchlaufen werden. Eine bestimmte Region kann aus verschiedenen Gründen verworfen werden:

• Eine Region R1 wird dann verworfen, wenn ihre MINDIST größer ist als die MINMAXDIST einer anderen Region R2, da sie den nächsten Nachbar dann nicht beinhalten kann. Diese Vorgangsweise wird auch als downward pruning bezeichnet.
• Wenn die tatsächliche Entfernung vom Anfragepunkt P zu einem gegebenen Objekt O größer ist als die MINMAXDIST einer Region, kann diese Region auch verworfen werden. Diese Strategie nennt man upward pruning.
• Außerdem kann man eine Region verwerfen, wenn ihre MINDIST größer ist als die tatsächliche Entfernung vom Anfragepunkt P zu einem Objekt O (upward pruning).

Rekursive Prozedur Nächste-Nachbar-Suche

Die Prozedur Nächste-Nachbar-Suche ist rekursiv implementiert. In dem Fall, dass der besuchte Knoten ein Blatt ist, wird der Knoten untersucht.

Blattknoten

If Node.type = LEAF then
	For I := 1 to Node.count
		/* Entfernung des Punktes zur Region berechnen */
		dist := objectDist(Pt, Node.region)
		/*	ist die berechnete Entfernung kleiner als die der vorigen
			Region, wird dieses Blatt als nächster Nachbar bestimmt */
		if (dist < Nearest.dist) then
			Nearest.dist := dist
			Nearest.region := Node.region

Auto

Es wird für alle Einträge des Knotens die Entfernung zwischen dem Anfragepunkt und der Region des untersuchten Knotens ermittelt. Ist diese neu ermittelte Entfernung kleiner als die aktuelle Entfernung, wird diese Region als die nächeste Region verwendet, der nächste Nachbar wurde gefunden.

Falls der besuchte Knoten in der Nächste-Nachbar-Suche kein Blattknoten ist, werden die besuchten Knoten geordnet, sortiert, ein downward und upward pruning durchgeführt und die Prozedur mit dem nächsten Sohn rekursiv aufgerufen, dessen Seitenregion dem Anfragepunkt am nächsten ist (siehe Kommentare im Programmcode):

innere Knoten

Else
	erzeugeSohnListe(Punkt, Knoten, sohnListe)
	/* Liste sortieren, damit der nächste Sohn zuerst ausgewählt werden kann */
	sortiereSohnListe(sohnListe)
	/* downward pruning durchführen */
	anzahl = pruneSohnListe(Knoten, Punkt, Nächster, sohnListe)
	For I := 1 to anzahl
		KnotenNeu := Knoten.aktuellerSohn
		/*mit nächstem Sohn der Verzweigung Suche weiterführen */
		nearestNeighborSearch(KnotenNeu, Punkt, Nächster)
		/* upward pruning durchführen */
		anzahl := pruneSohnListe(Knoten, Punkt, Nächster, sohnListe)

Stärken des SR-Baums

Die Stärken des SR-Baum420s bauen auf die Einteilung der Seitenregionen in Kreise und Rechtecke auf. Die Seitenregionen haben ein geringeres Volumen als im R*-Baum und im SS-Baum und der Durchmesser ist in etwa gleich gering wie im SS-Baum. Durch diese Eigenschaften kann der SR-Baum420 die Punkte in Regionen mit kleinerem Volumen und geringem Durchmesser aufteilen, die dadurch disjunkter sind. Durch die Reduzierung des Volumens und des Durchmessers erhöht sich außerdem die Performanz der Nächste-Nachbar-Suche.

Schwächen des SR-Baums

Ein Nachteil beim SR-Baum420 ist, dass der Aufwand für die Erzeugung höher ist, als beim SS-Baum. Ein weiteres Problem hängt mit dem Verzweigungsgrad des SR-Baum420s zusammen: Die Verzweigung eines Indexbaumes nimmt ab, je höher die Dimensionalität ist, da die Größe eines Eintrags in einem Knoten mit zunehmender Dimensionalität zunimmt. Da ein Knoteneintrag eines SR-Baum420s eine bounding sphere und ein bounding rectangle enthält, ist seine Größe jedoch drei Mal so groß wie zum Beispiel ein Knoteneintrag im SS-Baum, oder eineinhalb Mal so groß wie im R*-Baum. Deshalb beträgt der Verzweigungsgrad beim SR-Baum420 nur ein Drittel vom SS-Baum und zwei Drittel vom R*-Baum. Eine Reduzierung der Verzweigungen kann erfordern, dass bei Anfragen mehr Knoten gelesen werden müssen. Möglicherweise wird dadurch die Performanz bei Anfragen beeinträchtigt.

Bibliographie

2

Auto

Kat03