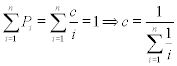content final ----TO DO: 1 Abb. draft - Bildbeschriftung(z.Z. mit Ignore ausgezeichnet)- Glossar und Akronymeinträge auszeichnen

Überblick

1

Entstehungsgeschichte des Zipfschen Gesetzes

• Benannt nach Sprachwissenschaftler George Kinsley Zipf
• Zipf untersuchte die statistische Verteilung von Wörtern in verschiedenen Sprachen
• Ermittlung der Häufigkeit für jedes Wort
• Ranking der Wörter nach deren Häufigkeit
• Zipf erhielt so für jede Sprache eine " Verteilung der Worthäufigkeit"
• Verblüffendes Ergebnis
  • " Verteilung der Worthäufigkeit" bei allen Sprachen praktisch ident
  • gleiches Ergebnis auch für " Verteilung der Buchstabenhäufigkeit"
• Zipfsches Gesetz ist mathematische Formulierung dieser empirisch beobachtbaren Gesetzmäßigkeit

2

Entstehungsgeschichte des Zipfschen Gesetzes

Das Zipfsche Gesetz ist benannt nach dem amerikanischen Sprachwissenschaftler George Kinsley Zipf (1902-1950). Er untersuchte die statistische Verteilung von Wörtern in verschiedenen Sprachen. Seine Untersuchungen gingen von der Kenntnis aus, dass es in jeder Sprache Wörter gibt, die besonders oft, andere wieder weniger oft genutzt werden. Für seine Untersuchungen erstellte er nun ein Ranking der Wörter einer Sprache: Das am häufigsten verwendete Wort reihte er an die erste Stelle, das zweithäufigste an zwei Stelle und so weiter. Jedem Wort ordnete er zusätzlich dessen empirisch ermittelten Häufigkeitswert zu. So erhielt er eine „Verteilung der Worthäufigkeit“ einer Sprache. Er verglich nun die Verteilung der Worthäufigkeit unterschiedlicher Sprachen, und kam zu dem verblüffenden Ergebnis, dass diese für alle Sprachen praktisch ident ist. Weitere Untersuchungen zeigten auch, dass die Verteilung der Buchstabenhäufigkeit in den unterschiedlichen Sprachen der gleichen Gesetzmäßigkeit gehorcht. Die mathematische Formulierung dieser empirisch beobachtbaren Gesetzmäßigkeit wird als Zipfsches Gesetz (Zipf Law) bezeichnet.

Beispiel: Ermittlung von Rang und Worthäufigkeit

Zur Demonstration, wie man die Verteilung der Worthäufigkeit eines beliebigen Textes ermittelt, untersuchen wir den oberen Text unter „Entstehungsgeschichte des Zipfschen Gesetzes“.

Der Absatz besteht aus exakt 150 Wörtern. Die am häufigsten darin vorkommenden Wörter sind der, die, er. Sie kommen jeweils 6-mal vor. Ihnen wird der Rang 1-3 zugewiesen. Die Worthäufigkeit errechnet sich aus:

Auf dem vierten Rang folgt das Wort Verteilung. Es kommt insgesamt 4-mal vor.

5. Rang: Das Wort in (3-mal):

6. – 8. Rang: Die Wörter ist, von, und (jeweils 2-mal):

Etc.

Anmerkung zum Beispiel Worthäufigkeit

Zu beachten ist bei diesem Beispiel, dass es nur veranschaulichen soll, wie Rang und Worthäufigkeit ermittelt werden. Der Text ist viel zu kurz, um aus ihm allgemein gültige statistische Gesetzmäßigkeiten ableiten zu können.

Mathematsche Formulierung des Zipfschen Gesetzes

1

Formel für das Zipfsche Gesetz

errechnet sich aus:

2

Formel für das Zipfsche Gesetz

...Rang eines Wortes

...Häufigkeit des Wortes vom Rang

...ist ungefähr eins. Im einfachen Fall kann angenommen werden, dass exakt eins ist.

…ergibt sich wie folgt ( ist die Anzahl aller vorhandenen Wörter, wird als 1 angenommen):

Zipfsches Gesetz in der Linguistik

1

Praktische Vorgangsweise

• Untersuchung eines hinreichend langen deutschsprachigen Textes
  • Für jedes Wort wird Häufigkeit ermittelt
  • Wörter nach deren Häufigkeit gereiht
    • Das häufigste Wort wird auf Rang 1 gestellt
    • das zweit häufigste auf Rang 2 etc.

Verteilung der Worthäufigkeit in der deutschen Sprache

1. UND (0,084) – 2. DIE (0,054) – 3. DER (0,054) – 4. IN (0,022)– 5. WIR (0,017) – 6. ZU (0,016)– 7. FÜR (0,015)– 8. SIE (0,013)– 9. VON (0,013) – 10. DEN (0,012) – 11. DES (0,011)– 12. IST (0,011)– 13. EINE (0,010) - 14. NICHT (0,010)

Vergleich Verteilung der Worthäufigkeit/Zipfsches Gesetz

• Diagrammerläuterung
  • Blau Linie - Werte errechnet mit Zipfschen Gesetz
  • Rot Linie - Empirisch ermittelte Werte
• Diagrammdiskussion
  • Rang kleiner 10 - ungenaue Näherung
  • Rang größer 10 - sehr genaue Näherung
  • Für sehr hohe Ränge - ungenaue Näherung (in Abbildung nicht ersichtlich)

2

Praktische Vorgangsweise

Man betrachte einen für eine statistische Untersuchung hinreichend langen deutschsprachigen Text, und untersucht, mit welcher Häufigkeit die verschiedenen Wörter darin vorkommen. Anschließend ordnet man die Wörter nach deren Häufigkeit. Das häufigste Wort wird auf Rang 1 gestellt, das zweit häufigste auf Rang 2 und sofort.

Verteilung der Worthäufigkeit in der deutschen Sprache

Im Folgenden Das Ranking der 14 häufigsten deutscher Wörter (in Klammer deren Worthäufigkeit):

1. UND (0,084) – 2. DIE (0,054) – 3. DER (0,054) – 4. IN (0,022)– 5. WIR (0,017) – 6. ZU (0,016)– 7. FÜR (0,015)– 8. SIE (0,013)– 9. VON (0,013) – 10. DEN (0,012) – 11. DES (0,011)– 12. IST (0,011)– 13. EINE (0,010) - 14. NICHT (0,010)

Vergleich Verteilung der Worthäufigkeit/Zipfsches Gesetz

Die Abbildung zeigt die Verteilung der Worthäufigkeiten eines deutschen Textes in Abhängigkeit vom Wort-Rang (rote Linie). Die Blaue Linie ist die Kurve, die sich durch das Zipfsche Gesetz ergibt. Aus dem Diagramm kann man erkennen, dass das Zipfsche Gesetz die Worthäufigkeit der ersten 10 Ränge ungenau, die der folgenden Ränge allerdings sehr präzise beschreibt. Es sei hier angemerkt, dass auch sehr hohe Ränge durch das Zipfsche Gesetz nur mehr unzureichend beschrieben werden.

Worthäufigkeit: rote Linie – Ranking deutsche Wörter; blaue Linie – Zipfsches Gesetz [zipf2005]

Zipfsches Gesetz jenseits der Linguistik

1

Allgemeine Bedeutung des Zipfschen Gesetzes

• Grundprinzip von Zipf -
  • Weniger Wörter werden sehr oft verwendet
  • Viele Wörter werden selten verwendet
• Zipfsche Gesetz auch außerhalb der Linguistik gültig
  • Das Zipfschen Gesetz ist dabei eng verwandt mit
    • Pareto-Prinzip
    • 80:20 Regel

Pareto-Prinzip

• Ein kleiner Teil von Elementen trägt einen großen Teil des Gesamtwertes
• Ein großer Teil der Elemente trägt nur einen geringen Teil des Gesamtwertes

Die 80:20 Regel

• 20% der Elemente tragen zu 80% des Gesamtwertes bei
• 80% der Elemente tragen zu 20% des Gesamtwertes bei

Beispiele zur 80:20 Regel

• Symbolsequenzen einer DNA
• Aufwände bei Projekten
• Wohlstandsverteilung auf die Weltbevölkerung
• Größe von menschlichen Siedlungen
• Dateigrößen im Internet
• Aufrufhäufigkeit von Webseiten
• Verteilung von Requests auf multimediale Dateien

2

Allgemeine Bedeutung des Zipfschen Gesetzes

Das Auffallende an der Zipfschen Häufigkeitsverteilung ist, dass in allen Sprachen nur sehr wenige Wörter sehr oft verwendet werden, viele Wörter hingegen nur selten. Es hat sich gezeigt, dass das Zipfsche Gesetz auch in vielen Bereichen außerhalb der Linguistik seine Gültigkeit hat. Das Zipfschen Gesetz ist dabei eng mit dem Pareto-Prinzip (80:20 Regel) verwandt.

Pareto-Prinzip

Das Pareto-Prinzip beschreibt die in vielen Bereichen beobachtbare Gesetzmäßigkeit, dass nur ein kleiner Teil von Elementen einen großen Teil des Gesamtwertes trägt, hingegen ein großer Teil der Elemente nur einen geringen.

Die 80:20 Regel

Das Pareto-Prinzip lässt sich gut durch die 80:20 Regel beschreiben:

20% der Elemente tragen zu 80% des Gesamtwertes bei, die restlichen 80% der Elemente nur 20%

Beispiele zur 80:20 Regel

Die 80:20 Regel ist in den unterschiedlichsten Bereichen wieder zu finden:

• Symbolsequenzen einer DNA
• Aufwände bei Projekten: 20% des Gesamtaufwandes erfüllt 80% des Projektziels, die restlichen 80% des Aufwandes nur 20 %
• Wohlstandsverteilung auf die Weltbevölkerung
• Größe von menschlichen Siedlungen - der Großteil der Menschen leben in wenig großen Städten, verhältnismäßig wenige Menschen leben in den vielen kleinen Dörfern
• Dateigrößen im Internet
• Aufrufhäufigkeit von Webseiten
• Verteilung von Requests auf multimediale Dateien

3

Pareto-Prinzip

Weiterführender Link: Zipf, Power-laws, and Pareto - a ranking tutorial adam2002

Beispiele zur 80:20 Regel

Weiterführender Link: Zipf’s law and the Internet adam2002-1

Akronyme

DNA - Deoxyribonucleic Acid (Dexoxyribonukleinsäure)

Glossar

80:20 Regel – siehe „Pareto-Prinzip“

Linguistik – Sprachwissenschaft

Pareto-Prinzip –benannt nach dem Italiener Vilfredo Pareto. Das Pareto-Prinzip beschreibt die in vielen Bereichen beobachtbare Gesetzmäßigkeit, dass nur ein kleiner Teil von Elementen einen großen Teil des Gesamtwertes trägt, hingegen ein großer Teil der Elemente nur einen geringen.