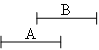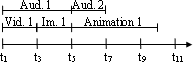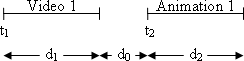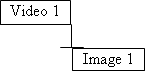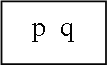| Title: | Modellierung der Struktur von Multimedia-Daten - Zeitliche und räumliche Modelle | ||
|---|---|---|---|
| Abstract: | In dieser LU wird auf die zeitliche und räumliche Datenmodellierung eingegangen. Neben der Definition zeitlicher und räumlicher Beziehungen werden verschiedene Modellierungsmethoden erläutert. | ||
| Status: |
Formeln rendern. |
Version: | 7.0 |
| History: |
Rechtschreibfehler gecheckt (LOD 1+2) Acronyme, "",-- done Links auf LU Temporale und Räumliche Komposition in Modul 3 done. Sourcecode repariert. Unbekannte Character gecheckt. |
||
| Author 1: | Bernhard Tatzmann | E-Mail: | bernhard@isys.uni-klu.ac.at |
|---|---|---|---|
| Author 2: | (empty) | E-Mail: | (empty) |
| Author 3: | (empty) | E-Mail: | (empty) |
| Author 4: | (empty) | E-Mail: | (empty) |
| Author 5: | (empty) | E-Mail: | (empty) |
| Organization: | Universität Klagenfurt - Institut für Informatik-Systeme | ||
Einleitung1AutoModellierung von Zeit und Raum stellt die Grundlage für die moderne multimediale Datenmodellierung dar. 2AutoHerkömmliche Verfahren sind für die Modellierung multimedialer Daten nicht mehr ausreichend. Da diese Daten auf den Dimensionen Zeit und Raum basieren, stellt deren Modellierung die Grundlage für die moderne multimediale Datenmodellierung dar. Zeitliche Datenmodelle1EinleitungZeitliche Beziehungen bilden die Grundlage der zeitlichen Datenmodelle:
Definitionen zeitlicher BeziehungenArten zeitlicher Beziehungen:
7 zeitliche Beziehungen nach Allen All83
AutoDiese beiden Arten der Beschreibung erlauben jedoch keine exakten quantitativen Aussagen. Modellierung zeitlicher Beziehungen
Hard Temporal Models
Timeline Modell
Auto PC
Auto PDA_Phone
Auto
Timed Petri Nets
Auto PC
Auto PDA_Phone
Flexible Temporal ModelsHier werden keine exakten Zeitpunkte für die Beginn- und Vorführungszeiten, sondern Zeitintervalle angegeben. Auto PC
Auto PDA_Phone
Auto Um konkrete Werte für die benötigten Parameter zu bekommen ist es nötig, die Ungleichungen zu lösen. Flexible Interactive Presentation Synchronization (FLIPS)Flexible Interactive Presentation Synchronization (FLIPS487) SKD95 bietet eine weitere Möglichkeit der flexiblen zeitlichen Modellierung. 2 Methoden zur zeitlichen Synchronisierung definiert:
Barriere: Eine
Ereignis
Auto PC
Auto PDA_Phone
AutoEnabler: Das Ereingis A 1 wird als Enabler des Ereignisses B 1 bezeichnet, wenn das Auftreten von A 1 B 1 auslöst (A 1 -> B 1 ).
Auto PC
Auto PDA_Phone
2EinleitungWährend räumliche Modelle für graphische Datenbanken und Bilddatenbanken ausreichend waren, stellen zeitbasierte Medien neue Anforderungen an die Datenmodellierung. Die Grundlage für zeitliche Datenmodelle bilden die verschiedenen Arten zeitlicher Beziehungen. Sie erlauben es, nach entsprechender Indizierung der Daten Suchbedingungen zu formulieren. Nach Definition der verschiedenen Möglichkeiten zeitlicher Beziehungen kann auf deren Modellierung eingegangen werden. Definitionen zeitlicher BeziehungenBei der Definition zeitlicher Beziehungen unterscheidet man zwischen jenen Beschreibungen, die sich auf den Vergleich zweiter Zeitpunkte beziehen, und jenen, die die Lage zweier Zeitintervalle beschreiben. Die relative zeitliche Lage zweier Zeitpunkte ist auf drei Möglichkeiten beschränkt: bevor (<), gleichzeitig (=), danach (>). Diese Art der zeitlichen Beziehungen werden laut Wahl und Rothermel WR94 im Englischen als "basic point relations" (basic PR485s) bezeichnet. Bei den zeitlichen Beziehungen zweier Zeitintervalle gibt es schon deutlich mehr Möglichkeiten. Allen All83 führt 13 verschiedene Möglichkeiten, in denen ein zeitlich geordnetes Paar von Zeitintervallen in Beziehung stehen kann, ein. In der folgenden Tabelle werden zunächst 7 verschiedene zeitliche Beziehungen, wie z.B. Zeitintervall A liegt vor Zeitintervall B, definiert: 7 zeitliche Beziehungen nach Allen All83
AutoZu diesen 7 Möglichkeiten kommen noch die inversen Varianten, abgesehen von gleichzeitig, hinzu. Somit ergeben sich die in All83 beschriebenen 13 Möglichkeiten. Da diese beiden Arten der Beschreibung zeitlicher Beziehungen zwar Auskunft über die relativen zeitlichen Zusammenhänge geben, jedoch keine exakten quantitativen Aussagen treffen, sind die im folgenden Abschnitt vorgestellten Modelle nötig Pra97. Modellierung zeitlicher BeziehungenBasierend auf den grundlegenden Arten der zeitlichen Beziehungen, die im vorigen Abschnitt erläutert wurden, können nun Modelle für zeitliche Beziehungen erstellt werden. Dabei kann bei jedem Modell angegeben werden, ob es eher Zeitpunkt oder Zeitintervall basiert ist, wenngleich in manchen Fällen eine genaue Zuordnung schwer fällt, da oft beide Arten von Beziehungen verwendet werden. In Pra97 werden die zeitlichen Modelle außerdem noch in "Hard Temporal Models" (fixe zeitliche Modelle) bzw. "Flexible Temporal Models" (flexible zeitliche Modelle) eingeteilt: Hard Temporal ModelsHard Temporal Models beschreiben Zeitintervalle mit exakten Angaben von Zeitpunkt und Zeitintervalllänge. Im Folgenden sollen nun einige prominente Vertreter dieses Modells vorgestellt werden. Timeline ModellIm Timeline Modell werden die Zeitintervalle entlang einer Zeitlinie exakt festgesetzt. Es werden exakte Zeitpunktangaben über den Beginn der Intervalle bzw. über deren Intervalllängen gemacht. Das Video 1 in Abbildung "Timeline Modell" beginnt z.B. zur Zeit t1 und dauert t3-t1. Es lassen sich also alle Intervallpaare bzgl. ihrer Beginnzeiten mit <, =, > in Verbindung setzen. Das Timeline Modell ist folgedessen eher zeitpunktbasiert. Auto PC
Auto PDA_Phone
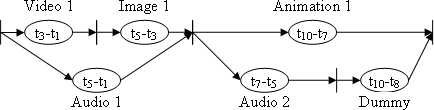
AutoDas Modell ist weit verbreitet, hat jedoch dadurch, dass es keine Angaben erlaubt, die sich auf die gesamten Längen zweier Zeitintervalle beziehen, einen gravierenden Nachteil. Es lässt sich z.B. nicht angeben, dass das Zeitintervall A während Zeitintervall B präsentiert werden soll Pra97. Timed Petri NetsIm Gegensatz zum Timeline Modell ist es mit Hilfe von Timed Petri Nets (TPN486) möglich, Beziehungen zwischen zwei Zeitintervallen anzugeben. Timed Petri Nets sind eine Erweiterung von Petri-Netzen und bieten somit eine Möglichkeit, temporale Geschehnisse in Form von grafischen Modellen darzustellen. Petri-Netze sind bipartite Graphen zur ereignisbasierten Modellierung von Systemabläufen, die aus Stellen-(places) und Transitions-(transitions) Knoten bestehen. Während Stellen durch Kreise symbolisiert werden und Bedingungen repräsentieren, werden Transitionen als vertikale Balken dargestellt und repräsentieren Ereignisse. Durch das Hinzufügen von Marken (tokens) zu Stellen, wird der aktuelle Systemzustand repräsentiert. Abhängig von der Anzahl der Marken am Eingang einer Transition können diese schalten (firing), wodurch die Marken weiterbewegt werden und somit der Zustand der Systems verändert wird. Dieser Prozess erfolgt nach genauen Regeln, auf die hier jedoch nicht näher eingegangen wird. Weitere Informationen zum dynamischen Verhalten von Petrinetzen finden sich in LU Temporale Komposition über OCPN in Modul 3 Link. Verwendet man Petri-Netze zur temporalen Darstellung von Multimediadaten, dann repräsentieren Stellen die Vorführung und Transitionen zeigen das Ende der Vorführung an. Mittels der Transitionen lässt sich die Synchronisation von verschiedenen Zeitintervallen darstellen. Die Vorführungszeiten werden als Labels innerhalb der Stellen platziert. Timed Petri Nets sind also intervallbasiert. Abbildung Timed Petri Nets zeigt das Beispiel aus Abbildung "Timeline Modell" als TPN486s. Wie man in der Abbildung sehen kann synchronisieren die Transitionen (vertikale Balken) die Vorführungsintervalle. Die Vorführungen Audio 1 und Video 1 beginnen nach dieser Definition also gleichzeitig. Die Intervalllängen ergeben sich durch die Beschriftungen der Stellen (Kreise). Das Vorführungsintervall Audio 1 dauert gleich lange wie die beiden Intervalle Video 1 und Image 1 zusammen. Um zeitliche Beziehungen von Intervallen zu definieren, die nicht gleichzeitig beginnen oder enden, werden Dummy-Stellen eingefügt. Auto PC
Auto PDA_Phone
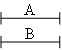
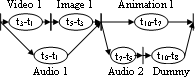
Flexible Temporal ModelsIm Gegensatz zu den obigen Modellen werden bei den flexiblen Zeitmodellen keine exakten Zeitpunkte für die Beginn- und Vorführungszeiten, sondern Zeitintervalle angegeben. Prabhakaran Pra97 gibt für die zeitliche Beziehung "Video 1 vor Animation 1" (siehe folgende Abbildung) folgende Zeitintervalle an: Auto PC
Auto PDA_Phone
Auto Für das Zeitintervall
Für das Zeitintervall
Und schließlich gelten für die Vorführungsdauer von Video 1 bzw.
Animation 1 die unteren und oberen Schranken
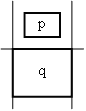
Prabhakaran Pra97 nennt diese Art der Intervalldeklaration "value range specification". Da moderne Multimediale Informationssysteme auf der Interaktion mit dem Benutzer aufgebaut sind, ist es von Vorteil, wenn gewisse zeitliche Freiheiten bestehen. Um konkrete Werte für die benötigten Parameter zu bekommen ist es jedoch nötig, die Ungleichungen zu lösen. Flexible Interactive Presentation Synchronization (FLIPS)Flexible Interactive Presentation Synchronization (FLIPS487) SKD95 bietet eine weitere Möglichkeit der flexiblen zeitlichen Modellierung. In FLIPS487 sind zwei Methoden zur zeitlichen Synchronisierung definiert: Barriere und Enabler. Barriere: Eine
Ereignis Ein Beispiel hierfür wäre z.B. die Präsentation zweier Videos, die
sich dieselbe Hardware teilen. Dann gilt das Ende von Video 1 ( Auto PC
Auto PDA_Phone
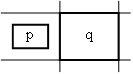
AutoEnabler: Das Ereingis A 1 wird als Enabler des Ereignisses B 1 bezeichnet, wenn das Auftreten von A 1 B 1 auslöst (A 1 -> B 1 ). Eine Animation, die von einer Musik begleitet wird, die enden soll, wenn die Animation endet, würde eine Anwendungsmöglichkeit für einen Enabler bieten. Das Ereignis "Ende der Animation" müsste das Ereignis "Ende der Musik" freigeben (siehe folgende Abbildung). Auto PC
Auto PDA_Phone
Weitere Modelle zur zeitlichen ModellierungNeben den oben erwähnten existiert eine Vielzahl anderer Modelle zur zeitlichen Modellierung z.B.: Temporal Point Nets BZ93 und Path Expressions CH74. Weitere Informationen zur zeitlichen Modellierung finden sich in Strukturmodelle für temporale Komposition. 3Zeitliche BezeihungenWeitere Literatur zu zeitlichen Beziehungen bieten LG93 und TS04. Timed Petri NetsPetri Nets World - http://www.daimi.au.dk/PetriNets/ Räumliche Datenmodelle1Einleitung
Minimal Bounding Rectangles (MBR418s):
Man unterscheidet auch hier zwischen:
Pra97 PC
Pra97 PDA_Phone
AutoBeziehungen zwischen MBR418s unterteilen sich in: Richtungsbeziehungen:
Topologische Beziehungen:
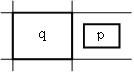
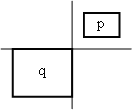
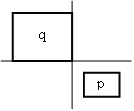
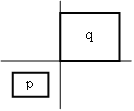
Richtungsbeziehungen und topologische Beziehungen
AutoBsp. für Frames einer Webanwendung:
Auto PC
Auto PDA_Phone
AutoDistanzcharakteristik:
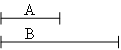
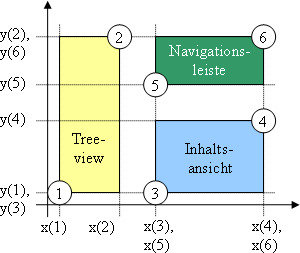
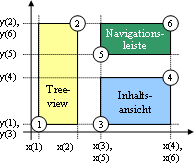
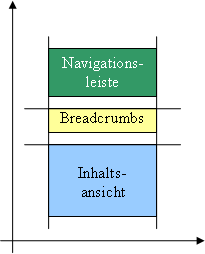
2EinleitungRäumliche Datenmodelle erweitern die zeitlichen Modelle um, zwei weitere Dimensionen. Die räumliche Beschreibung von Objekten in den Mediendaten wird meist mit Hilfe von Rechtecken durchgeführt. Dies kann einerseits zur Beschreibung von Anordnungen visueller Daten bei der Darstellung dienen, sowie für Abfragetechniken visueller Daten benützt werden. Besonders Minimal Bounding Rectangles (MBR418s) eignen sich durch ihre einfache Definition gut für Lagebeschreibungen der Objekte. Sie lassen sich durch Angabe der linken unteren sowie rechten oberen Ecke eindeutig definieren (siehe folgende Abbildung). Wie bei den zeitlichen Modellen unterscheidet Prabhakaran Pra97 auch hier zwischen, "hard spatial specification" (fixen Spezifikationen) und "flexibel spatial specification" (flexiblen Spezifikationen). Bei der Verwendung von fixen Spezifikationen könnte man das Rechteck der "Treeview" in untenstehender Beispielabbildung mit konkreten Werten wie z.B. x(1) = 5 und y(1) = 5 bzw. x(2) = 50 und y(2) = 20 definieren. Würde man die flexible Spezifikationsmethode verwenden müsste man die relativen Beziehungen der Begrenzungspunkte, wie z.B.: x(5)-x(1) <= 30 usw., definieren. Pra97 PC
Pra97 PDA_Phone
AutoLi et. al LOS96 unterteilen Beziehungen zwischen MBR418s in Richtungs- bzw. topologische Beziehungen. Wobei sich die Richtungsbeziehungen wiederum in 3 Kategorien unterteilen:
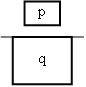
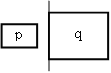
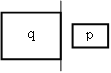
Die topologischen Beziehungen lauten: gleich, innerhalb, überdeckend, überlappend, außerhalb verbunden, disjunkt. Die folgende Tabelle fasst nochmals alle aufgezählten Beziehungstypen zusammen. Richtungsbeziehungen und topologische Beziehungen
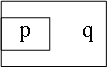
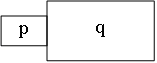
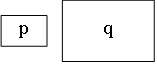
AutoLi et. al LOS96 geben noch einige Regeln für die eingeführten Richtungsbeziehungen, wie Reflexivität, Symmetrie, Transitivität usw., an. Die Transitivität besagt z.B.: Wenn Objekt B nördlich von Objekt A ist und Objekt C nördlich von Objekt B, so kann gesagt werden, dass auch Objekt C nördlich von A ist. Untenstehende Abbildung zeigt drei Frames einer Webanwendung die diese Beziehung erfüllen. Dies sei nur als kurzes Beispiel angegeben. Für eine vollständige Auflistung aller Regeln sei auf LOS96 verwiesen. Auto PC
Auto PDA_Phone
AutoIn WR94 wird noch eine weitere Art der räumlichen Beziehungsbeschreibung angegeben. Die dort beschriebene Distanzcharakteristik definiert den Abstand zweier Objekte. Hierbei wird zwischen Entfernungen innerhalb und außerhalb eines Objektes unterschieden. Beispiel: Objekt A ist außerhalb 5cm von Objekt B entfernt. Dies bedeutet, dass die beiden Objekte disjunkt sind und einen Abstand von 5cm haben. Weitere Informationen zur räumlichen Modellierung finden sich in Strukturmodelle für räumliche Komposition. 3Räumliche BeziehungenWeitere Referenz für räumliche Beziehungen: PT96 Bibliographie2AutoAll83 BZ93 CH74 LOS96 Pra97 PT96 SKD95 LG93 TS04 WR94 |
(
... Zeitraum vom Ende der Vorführung von Video 1 bis zum Beginn von
Animation 1)
( 
-
... Zeitraum zwischen den Beginnzeiten von Video 1 und Animation 1)
bzw. 
(
...
Vorführungsdauer von Video 1, 
...
Vorführungsdauer von Animation 1)
wird als Barriere für Ereignis B 1 bezeichnet (
), wenn Objekt B an der Stelle 
und 
liegen muss:
und 
liegen muss:
und 
bzw. 
und 
:
| (empty) |