Einführung Animation
 .
.
Einleitung
Das Wort Animation(lat. animatio = das Beleben) steht für ein Verfahren um unbelebten Objekten Bewegung zu verleihen
[s]
. Im Allgemeinen fasst man unter Animation alle Änderungen zusammen, die einen sichtbaren Effekt an einem Objekt bewirken. Dies sind Veränderungen von:
- Position (Bewegung)
- Form
- Farbe
- Transparenz
- Musterung
- Größe
- Kameraposition
- Beleuchtung
Veränderungen der Position werden unter dem Begriff Bewegungsdynamiksummiert, Veränderungen von Farbe, Transparenz, Musterung usw. nennt man Änderungsdynamik.
 .
.
Frames, Schlüsselbilder und Zwischenbilder
Eine Animation kann als Folge von Bildern gesehen werden. Die einzelnen Bilder nennt man Frames. Durch ein Abspielen der Frames, die sich mehr oder weniger voneinander unterscheiden, entsteht eine Art Film, also eine Animation. Werden die Bilder schnell genug abgespielt, so nimmt man keinen Übergang mehr wahr, die Abfolge erscheint kontinuierlich. Die Frames können in zwei Gruppen eingeteilt werden. Die Schlüsselbilder einerseits und die Zwischenbilder andererseits. Schlüsselbilder (Key Frames) sind Bilder, in denen die beinhalteten Objekte extreme bzw. wichtige Positionen annehmen. Zwischenbilder sind solche Frames, die den Übergang von einem Schlüsselbild auf das nächste darstellen
[s]
. Um Zwischenbilder in einer Animation zu erzeugen (sowohl für Bewegungs- als auch Änderungsdynamik), werden sogenannte Interpolationsverfahren angewendet. Das einfachste und intuitivste Interpolationsverfahren ist die lineare Interpolation (?Lerping?). Genaueres zu Interpolationsverfahren im Abschnitt Interpolation von Zwischenbildern.
Interpolation von Zwischenbildern.
 .
.
Bildrate und Double-Buffering
Damit Animationen flüssig erscheinen, also die Bilder nicht ruckartig wechseln, ist eine gewisse Mindestanzahl von Bildern pro Zeiteinheit erforderlich. Die Anzahl der Bilder pro Zeiteinheit nennt man Bildrate. Als Faustregel werden 24 Bilder pro Sekunde als Untergrenze gesehen, bei einfachen Animationen genügen aber unter Umständen auch weniger Bilder, bei anspruchsvollen Filmen ist die Bildrate höher
[s]
. In den folgenden Betrachtungen wird von 24 Bildern pro Sekunde ausgegangen. Werden pro Sekunde 24 Bilder angezeigt, so ist jedes Bild 1/24 Sekunden lang sichtbar. Wenn jedoch das Zeichnen eines Bildes alleine 1/24 Sekunden benötigt, ergibt sich folgendes Problem: Die zuerst gezeichneten Objekte (obere Teile des Bildes) sind 1/24 Sekunden lang sichtbar. Die zuletzt gezeichneten Objekte flackern nur kurz auf, und verschwinden danach wieder (werden wieder gelöscht), da schon das nächste Bild angezeigt wird. Man muss nun eine Möglichkeit finden, damit jedes Bild volle 1/24 Sekunden lang angezeigt wird
[s]
. Eine Möglichkeit hierfür ist das Double-BufferingKonzept.
Double-Buffering
Hier werden zwei unabhängige Framebuffer (Speicher für Bilder) verwendet. In der Animation aufeinanderfolgende Bilder werden in unterschiedlichen Buffern berechnet. Während das erste Bild (das sich im ersten Framebuffer befindet) gerade am Bildschirm angezeigt wird, wird schon das darauffolgende Bild im zweiten Framebuffer berechnet. Nach 1/24 Sekunden wird dann das Bild aus dem zweiten Framebuffer angezeigt und das nächste Bild im ersten Buffer berechnet. Somit ist sichergestellt, dass jedes Bild genau 1/24 Sekunden angezeigt wird
[s]
.
Transformation
Unter Transformation (geometrischer Transformation) werden drei Aspekte zusammengefasst: Translation, Skalierung und Rotation . Translation bedeutet Verschieben des Objektes in einem Koordinatensystem, Skalierung bedeutet Verändern der Größe (vergrößern, verkleinern) und unter Rotation versteht man das Drehen des Objektes. Da durch Transformationen also visuelle Effekte erreicht werden, sind sie auch für das Thema Animation von Relevanz. Auf eine genauere Beschreibung von 2D- und 3D-Transformationen wird hier aber verzichtet, stattdessen wird auf die Lerneinheit Mathematische Grundlagen verwiesen.
 .
.
Interpolation von Zwischenbildern
Speziellfür Bewegungen von Objekten von einem Punkt zum anderen, aber auch für Formveränderungen usw. stellt die automatische Generierung von Zwischenbildern einen wichtigen Aspekt dar. Diese Zwischenbilder können durch Interpolation erzeugt werden. Anschließend werden zwei Interpolationsverfahren für die Bewegung von Objekten besprochen.
Lineare Interpolation
Hier wird aus einem Anfangsframe und einem Endframe (und evtl. zusätzlichen wichtigen Schlüsselframes) eine Folge von Zwischenframes erzeugt. Das zu animierende Objekt bewegt sich hierbei auf einer Geraden (deshalb die Bezeichnung ?linear?) zwischen Anfangs- und Endposition, die im Anfangs- und Endframe spezifiziert sind.
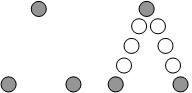 |
Das Problem beim Lerping liegt auf der Hand. Die dadurch generierte Bewegung ist oft nicht realitätsnah. Will man z.B. die Wurfparabel eines Balls animieren, hilft einem die spitze Bewegung (vgl. obige Abbildung) nicht weiter
[s]
.
Path-Following, Splines
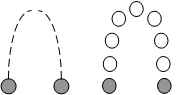
Path-Following soll den Problemen der linearen Interpolation entgegenwirken. Hier wird eine Kurve vorgegeben, an der sich das Objekt entlang bewegen soll. Beispielsweise gibt man hier nicht wie bei der linearen Interpolation die Anfangs- und Endframes an, sondern einen Pfad. Dieser Pfad sei beispielsweise eine Parabel. Demnach kann sich der Ball entlang der Parabel bewegen
[s]
.
 |
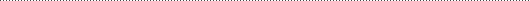
 .
.
Geschwindigkeitssteuerung
Sowohl bei der linearen Interpolation, als auch beim Path-Following müssen Überlegungen angestellt werden, mit welcher Geschwindigkeit sich das Objekt bewegen soll. Werden an der Geraden (beim Lerping) bzw. am Pfad (beim Path-Following) die einzelnen Zwischenbilder in gleichen Abständen positioniert, so bewegen sie sich mit konstanter Geschwindigkeit. Durch Positionieren der Bilder in unterschiedlichen Abständen am Pfad kann man Geschwindigkeitsänderungen simulieren. Um demnach eine Beschleunigung eines Objektes auf eine konstante Geschwindigkeit zu erzeugen, muss man zu Beginn die Zwischenbilder näher, im Verlauf der Bewegung weiter voneinander entfernt aneinander positionieren (konstante Entfernung). Mit diesem Vorgehen sind Geschwindigkeitsänderungen ohne merkbare sprunghafte Bildwechsel in der Animation erzielbar. Man nennt dieses Vorgehen easing( fairing, cushioning)
[s]
. Demnach ist ? ease-in, ease-out? ein Verfahren, bei dem ein Objekt zuerst beschleunigt wird, dann eine maximale Geschwindigkeit erreicht, und zum Schluss wieder gebremst wird.
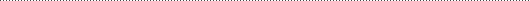
 .
.
Charakteristische Geschwindigkeitsfunktionen
Die Geschwindigkeit ist als Funktion darstellbar. Diese Funktion beschreibt, welche Strecke das Objekt in welcher Zeit zurücklegt und wird demnach Distance-Time-Function (Geschwindigkeitsfunktionen) genannt. Beim ease-in, ease-out Verfahren entspricht diese Funktion vom Kurvenverlauf etwa dem Sinus im Intervall [?p/2, +p/2]
[s]
. Weitere Beispiele für Geschwindigkeitsfunktionen sind in folgender Abbildung ersichtlich.
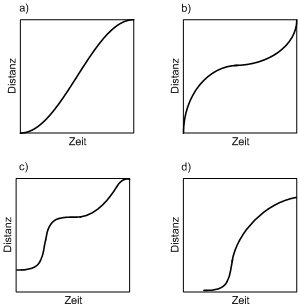 |
Ein sich auf der Kurve des Bildes a) bewegendes Objekt wird langsam beschleunigt und bremst zum Schluss wieder langsam ab (Ease-in, Ease-out). Bei b) beginnt das Objekt schnell, wird später abgebremst und beschleunigt gegen Ende wieder. Bild c) zeigt eine Kurve, bei der ein Objekt nicht am Beginn, sondern an einem späteren Punkt des Pfades anfängt sich zu bewegen. Im Bild d) steht das Objekt zu Beginn still. Es fängt erst ab einem späteren Zeitpunkt an, sich zu bewegen, und kommt auch nicht ans Ende der zurückzulegenden Distanz (oberer Kästchenrand). Generell kann die Steigung der Kurve als Geschwindigkeitsänderung betrachtet werden.
 .
.
Kamerapositionierung
Neben der Bewegung des Objektes spielt auch die Position der Kamera eine Rolle. Dies ist die Position, von der aus die Animation betrachtet wird. Am einfachsten ist es, die Kamera an einem bestimmten Punkt innerhalb der Animation zu fixieren. Dieser Punkt ist fest im Bild verankert und bewegt sich nie. Eine andere Möglichkeit ist die Positionierung an einem Punkt eines Objektes. Somit bewegt sich die Kamera immer mit dem animierten Objekt mit, was für bestimmte Anwendungsfälle wünschenswert sein kann. Die größtmögliche Flexibilität in der Betrachtung der animierten Objekte wird aber durch einen eigenen Kamerapfad erreicht. Wie für animierte Objekte wird hier ein eigener Pfad für die Kamera zur Verfügung gestellt, auf dem sich diese fortbewegt. Somit kann wieder mit Beschleunigungsprinzipien gearbeitet werden, um die Kamera zu bestimmten Zeitpunkten an bestimmten Punkten zu positionieren. Diese Variante ist vor allem dann nötig, wenn die Kamera zu unterschiedlichen Zeitpunkten unterschiedliche Objekte beobachten muss. Man spricht hierbei von Camera-Path-Following
[s]
.
 .
.
Morphing
Unter Morphing versteht man 2D-Image-Metamorphosen. Der Begriff Metamorphose bedeutet hierbei die Verwandlung von einem Bild (Quell-Bild, source-image) in ein anderes Bild (Ziel-Bild, destination-image). Ebenso wie beispielsweise Lerping ist auch das Morphing ein Interpolationsprozess. Nur beschreibt dieser nicht die Bewegung eines Objekts, sondern wie gesagt die Veränderung. Um eine möglichst gute Verwandlung zu ermöglichen, müssen zwischen Quell- und Zielbild bestimmte Korrespondenzen (Übereinstimmungen, Gemeinsamkeiten) bestehen (diese werden meist vom Benutzer angegeben). Im Folgenden wird eine Variante des Morphings beschrieben, das sogenannte Koordinatengitter-Morphing
[s]
.
 .
.
Koordinatengitter-Morphing
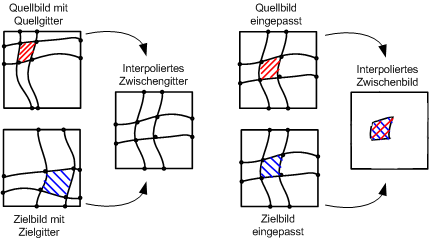
Hier wird sowohl über das Startbild, als auch das Endbild ein Koordinatengitter gelegt (vgl. Quell- und Zielgitter in der Abb.). Dabei hat jedes der beiden Gitter gleich viele Kreuzungspunkte und demnach auch gleich viele Zellen. Der Benutzer ist dafür verantwortlich, dass die korrespondierenden Elemente der beiden Bilder (rot und blau schraffierte Bereiche in der Abb.) in korrespondierenden Zellen der beiden Gitter liegen. Um nun ein Zwischenbild zu erzeugen, werden Quell- und Zielgitter auf ein Zwischengitter interpoliert. Danach wird sowohl das Quellbild in dieses Zwischengitter eingepasst, als auch das Zielbild in ein selbes Zwischengitter. Die Einpassung erfolgt durch Strecken bzw. Kontrahieren der Bildinhalte. Es wird also der Inhalt jeder Zelle in die Zelle des Zwischengitters eingepasst. Anschließend werden die so entstandenen zwei Teilbilder ?übereinander gelegt? wodurch sich das tatsächliche Zwischenbild ergibt (interpoliertes Zwischenbild in Abb.). Das ?Übereinanderlegen? erfolgt durch spezielle Berechnungen auf Pixelebene
[s]
.
 |
Das einzige was der Benutzer also tun muss, ist das Erstellen der Gitter für Ausgangs- und Endbild. Wie gerade beschrieben, wird eine Menge von Zwischenbildern interpoliert. Die Interpolation wird automatisiert durchgeführt. Das Ergebnis der Interpolation hängt entscheidend von der Qualität der vom Benutzer erstellten Gitter ab
[s]
. Werden nun alle Bilder nacheinander abgespielt, ist die Verwandlung des Startbildes ins Endbild als kontinuierliche Folge (wie ein Film) sichtbar. Anstatt Koordinatengitter anzugeben, gibt es auch Morphing-Verfahren, bei denen der Benutzer einfach korrespondierende Punkte zwischen den zwei Bildern angeben muss.